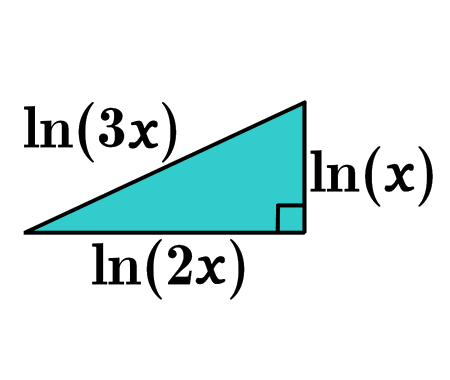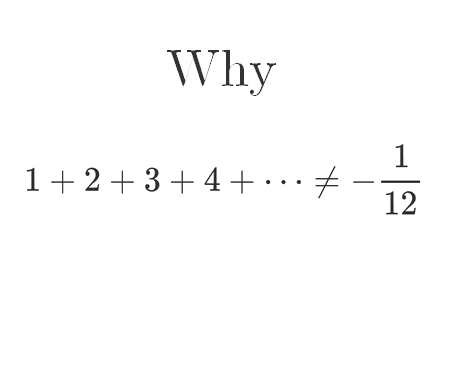Why 1+2+3+4+... is not equal to -1/12
Home -> Solved problems -> Why 1+2+3+4+… is not equal to -1/12

Solution
\(s\epsilon C\), The Zeta function \(\zeta\) converges for \(\operatorname{Re}(s)>1\)
\begin{aligned}
& \zeta(s)=\sum_{n=1}^{\infty} \frac{1}{n^s} \quad \operatorname{Re}(s)>1 \\\\
& \zeta(s)=1+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+\cdots \\\\
& \zeta(-1)=1+\frac{1}{2^{-1}}+\frac{1}{3^{-1}}+\frac{1}{4^{-1}}+\cdots \\\\
& \zeta(-1)=1+2+3+4+\cdots\\\\
\end{aligned}
But \(\operatorname{Re}(s)=-1<1\) ! Not allowed!!!
The functional equation of the Zeta function and Gamma function presents a representation of the Zeta function and not the real values of it, the real values are given for \(\operatorname{Re}(s)>1\) in the function \(\zeta(s)=\sum_{n=1}^{\infty} \frac{1}{n^s}\) :
\[\begin{aligned}
&\zeta(s)=2^s \pi^{s-1} \sin \left(\frac{\pi s}{2}\right) \Gamma(1-s) \zeta(1-s) \ \ \ \
s\epsilon C\backslash\left\{0,1\right\}
\end{aligned}\]
Now, let’s find out how to get \(\frac{-1}{12}\) which is equal to \(\zeta(-1)\) and not to \(1+2+3+4+…\)
\[\begin{gathered}
\zeta(-1)=2^{-1} \pi^{-2}(-1) \Gamma(2) \zeta(2) \\\\
\Gamma(2)=(2-1) !=1\\\\
\zeta(2)=1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\cdots=\frac{\pi^2}{6}\ (Basel \ problem) \\\\
\zeta(-1)=2^{-1} \pi^{-2}(-1) \cdot 1 \cdot \frac{\pi^2}{6}=-\frac{1}{12}
\end{gathered}
\]
Home -> Solved problems -> Why 1+2+3+4+… is not equal to -1/12
Every problem you tackle makes you smarter.
↓ Scroll down for more maths problems↓
Find the equation of the curve formed by a cable suspended between two points at the same height
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?
Is it possible to solve for \(x\) so that \(ln(x)\), \(ln(2x)\), and \(ln(3x)\) form a right triangle?