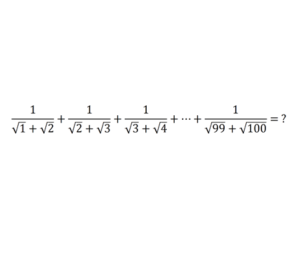Home -> Solved problems -> Calculate the sum
Calculate the sum
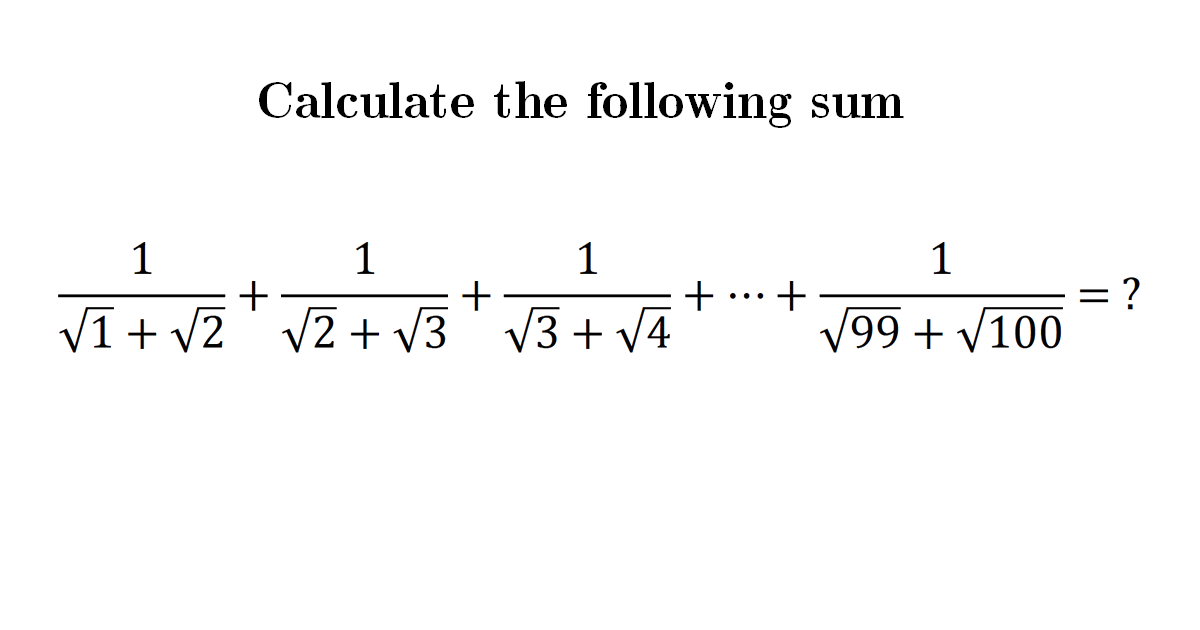
Solution
\[\begin{aligned}
& \frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{4}}+\cdots \cdot+\frac{1}{\sqrt{99}+\sqrt{100}}=\\\\
=& \frac{1}{\sqrt{1}+\sqrt{2}} \cdot \frac{-\sqrt{1}+\sqrt{2}}{-\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}} \cdot \frac{-\sqrt{2}+\sqrt{3}}{-\sqrt{2}+\sqrt{3}}+\cdots .+\frac{1}{\sqrt{99}+\sqrt{100}} \cdot \frac{-\sqrt{99}+\sqrt{100}}{-\sqrt{99}+\sqrt{100}}\\\\
=& \frac{-\sqrt{1}+\sqrt{2}}{-1+2}+\frac{-\sqrt{2}+\sqrt{3}}{-2+3}+\cdots+\frac{1}{-99+100}\\\\
=&-\sqrt{1}+\sqrt{2} -\sqrt{2}+\sqrt{3}-\sqrt{3}+\sqrt{4}-\sqrt{4}+\ldots+\sqrt{99}-\sqrt{99}+\sqrt{100}\\\\
=& 10-1\\\\
=&9
\end{aligned}\]
Home -> Solved problems -> Calculate the sum
Every problem you tackle makes you smarter.
↓ Scroll down for more math problems↓
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
Home -> Solved problems -> Calculate the sum
Share the solution: Calculate the sum