Home -> Solved problems -> Infinitely nested radicals posed by Ramanujan
Infinitely nested radicals posed by Ramanujan
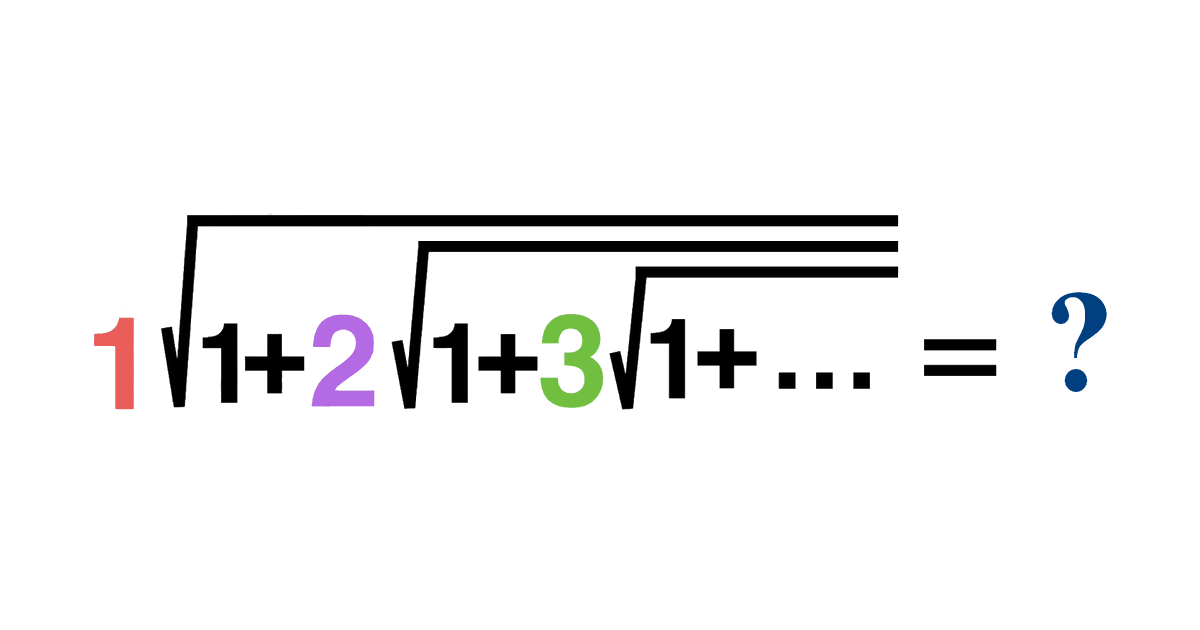
Solution
Solution by the mathematician Srinivasa Ramanujan :
\[n(n+2)=n\sqrt{1+(n+1)(n+3)}\] Let \(n(n+2)=f(n)\)
Thus, we see that \[\begin{aligned}
f(n) &=n \sqrt{1+f(n+1)} \\\\
&=n \sqrt{1+(n+1)\sqrt{1+f(n+2)}}\\\\
&=n \sqrt{1+(n+1)\sqrt{1+(n+2)\sqrt{1+f(n+3)}}}\\\\
&=n \sqrt{1+(n+1)\sqrt{1+(n+2)\sqrt{1+(n+3)\sqrt{1+\cdot\cdot\cdot}}}}
\end{aligned}\]
\[\Rightarrow n(n+2)=n \sqrt{1+(n+1)\sqrt{1+(n+2)\sqrt{1+(n+3)\sqrt{1+\cdot\cdot\cdot}}}}
\]
Putting \(n=1
\), we get \[\large \sqrt{1+2\sqrt{1+3\sqrt{1+\cdot\cdot\cdot}}}=3
\]
Like & Share the solution on Facebook :
Home -> Solved problems -> Infinitely nested radicals posed by Ramanujan
Related Topics
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
Home -> Solved problems -> Infinitely nested radicals posed by Ramanujan