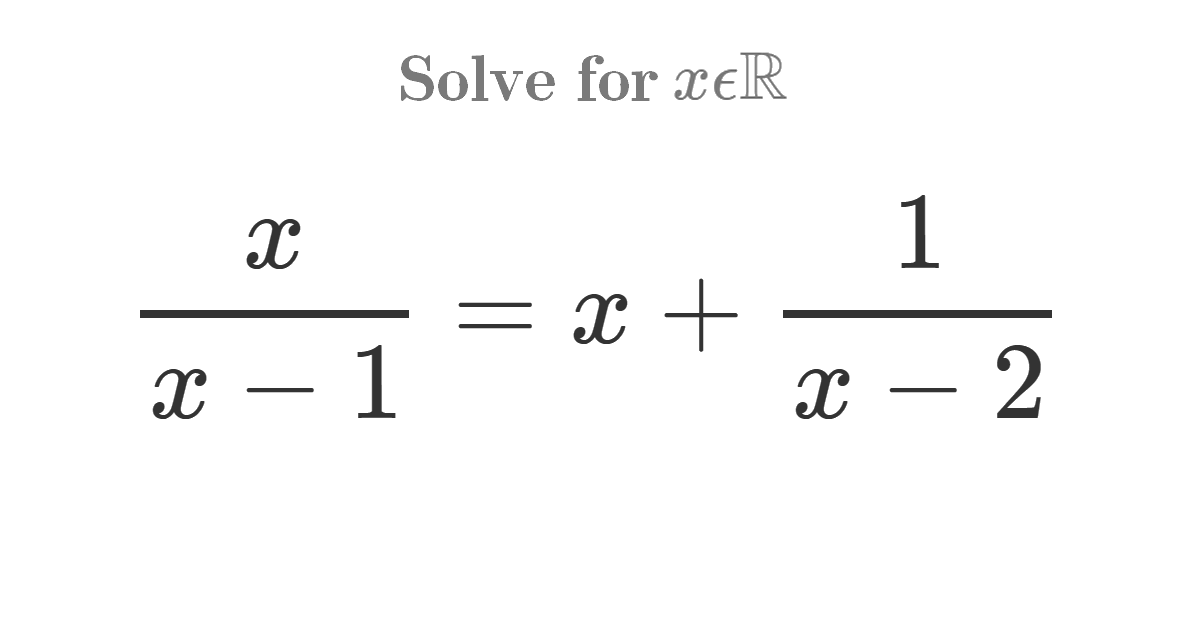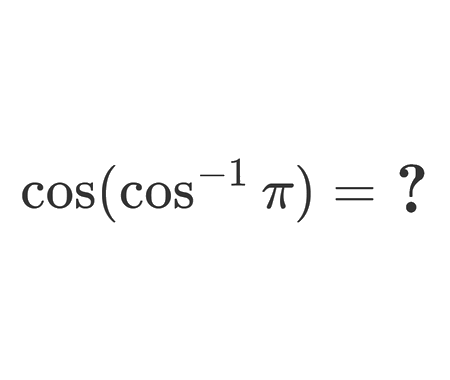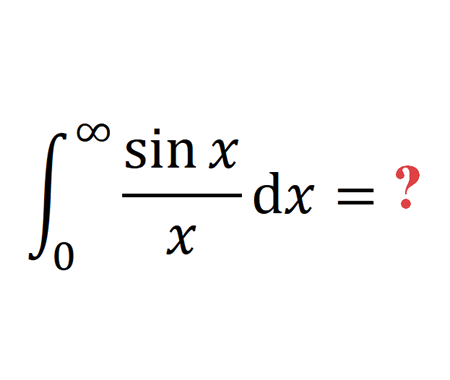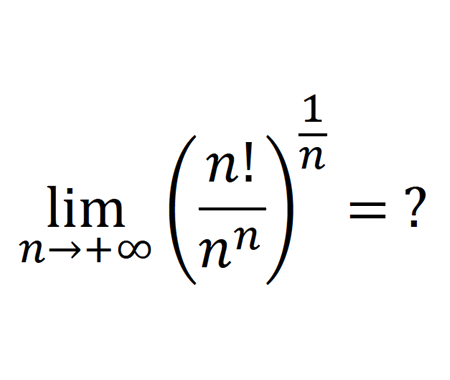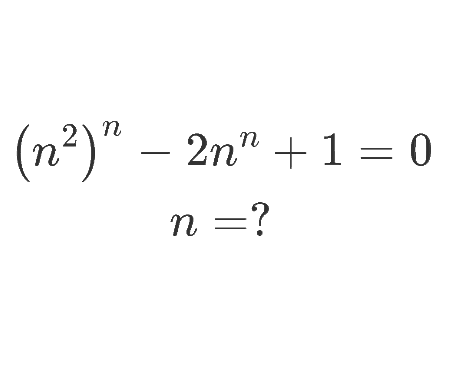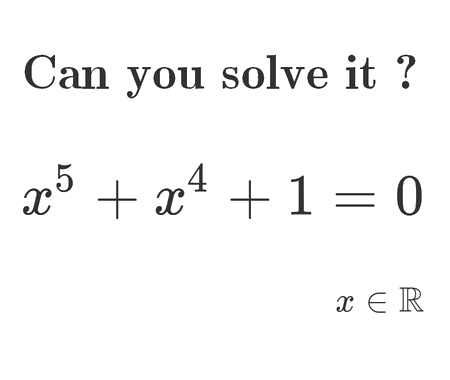Solve the equation for \(x\epsilon\mathbb{R}\) (Cubic equation Cardano’s method)
Solution
To solve the equation, let’s start by multiplying both sides by \(\left(x-1\right)\left(x-2\right)\) and simplifying, we get \[\frac{x}{x-1}\left(x-1\right)\left(x-2\right)=\left(x+\frac{1}{x-2}\right)\left(x-1\right)\left(x-2\right)\;\;\;\;\;\;\;,\;x\neq1\;and\;x\neq2\] \[\Rightarrow x\left(x-2\right)=x\left(x-1\right)\left(x-2\right)+x-1\] \[\Rightarrow x^{2}-2x=x^{3}-2x^{2}-x^{2}+2x+x-1\] \[\Rightarrow x^{3}-4x^{2}+5x-1=0\] Let \(f\left(x\right)=x^{3}-4x^{2}+5x-1\). \[\] Now we are dealing with a cubic equation, this can be made by replacing \(x\) by \(y+\frac{4}{3}\) to get rid of \(x^{2}\) term, this gives \[\left(y+\frac{4}{3}\right)^{3}-4\left(y+\frac{4}{3}\right)^{2}+5\left(y+\frac{4}{3}\right)-1=0\] \[y^{3}+3y^{2}\frac{4}{3}+3y\left(\frac{4}{3}\right)^{2}+\left(\frac{4}{3}\right)^{3}-4\left(y^{2}+2y\frac{4}{3}+\left(\frac{4}{3}\right)^{2}\right)+5y+\frac{20}{3}-1=0\] \[y^{3}+4y^{2}+\frac{16}{3}y+\frac{64}{27}-4y^{2}-\frac{32}{3}y-\frac{64}{9}+5y+\frac{20}{3}-1=0\] \[\Rightarrow y^{3}-\frac{1}{3}y+\frac{25}{27}=0\] We get a depressed cubic equation, to solve it we assume that \(y=s-t\) is a solution to the equation \(y^{3}+Ay+B=0\) with \(A=-\frac{1}{3}\) and \(B=\frac{25}{27}\), we get \[\left(s-t\right)^{3}+A\left(s-t\right)+B=0\] \[s^{3}-3s^{2}t+3st^{2}-t^{3}+As-At+B=0\] \[B+s^{3}-t^{3}-s\left(3st-A\right)+t\left(3st-A\right)=0\] \[\Rightarrow B+s^{3}-t^{3}+\left(A-3st\right)\left(s-t\right)=0\]
At this point we impose the condition \(A-3st=0\) following Cardano’s method, this helps to remove the fourth term in the previous equality, therefore we obtain a system of equations, we get \[B+s^{3}-t^{3}=0\] \[A-3st=0\] Writting \(s=\frac{A}{3t}\) and using the first equation of the previous system, we get \[B+\left(\frac{A}{3t}\right)^{3}-t^{3}=0\] To solve that, let’s make a variable change using \(u=t^{3}\), we get \[B+\frac{A^{3}}{27u}-u=0\] Multiplying by \(u\) with \(u\neq0\) gives a quadratic equation \[u^{2}-Bu-\frac{A^{3}}{27}=0\] Let’s substitute \(A\) and \(B\) with their values, we get \[u^{2}-\frac{25}{27}u+\frac{1}{729}=0\] Solving for \(u\) gives \[u=\frac{25+3\sqrt{69}}{54}\] Here we used only the larger solution, the other solution also works. This gives \[t=\frac{1}{3}\sqrt[3]{\frac{25+3\sqrt{69}}{2}}\] \[and\] \[s=\frac{A}{3t}=-\frac{1}{3}\sqrt[3]{\frac{2}{25+3\sqrt{69}}}\] Hence, the solution \[x=y+\frac{4}{3}=s-t+\frac{4}{3}\] \[x=\frac{4}{3}-\frac{1}{3}\sqrt[3]{\frac{2}{25+3\sqrt{69}}}-\frac{1}{3}\sqrt[3]{\frac{25+3\sqrt{69}}{2}}\approx0.24\] Now, let’s be sure that it is the only solution. To make this, we calculate the derivative \[f’\left(x\right)=3x^{2}-8x+5=\left(x-1\right)\left(3x-5\right)\] It is positive in \(\left(-\infty,1\right)\), negative in \(\left(1,\frac{5}{3}\right)\) and positive in \(\left(\frac{5}{3},\infty\right)\). Since \(f\left(1\right)=1\) and \(f\left(\frac{5}{3}\right)=\frac{23}{27}\), the function \(f\) is positive in \(\left[1,\infty\right)\) and has only one zero which is \(x\approx0.24\) in \(\left(-\infty,1\right)\).
Home -> Solved problems -> Solve for real x
Every problem you tackle makes you smarter.
↓ Scroll down for more maths problems↓
↓ ↓
↓ ↓
↓ ↓
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
Home -> Solved problems -> Solve for real x