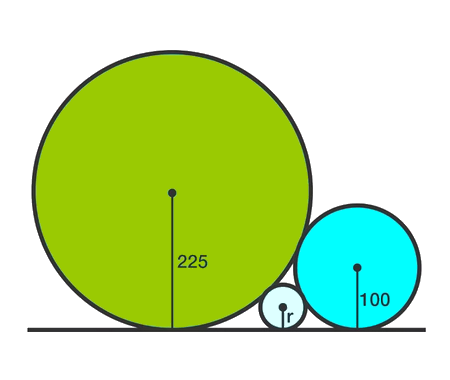
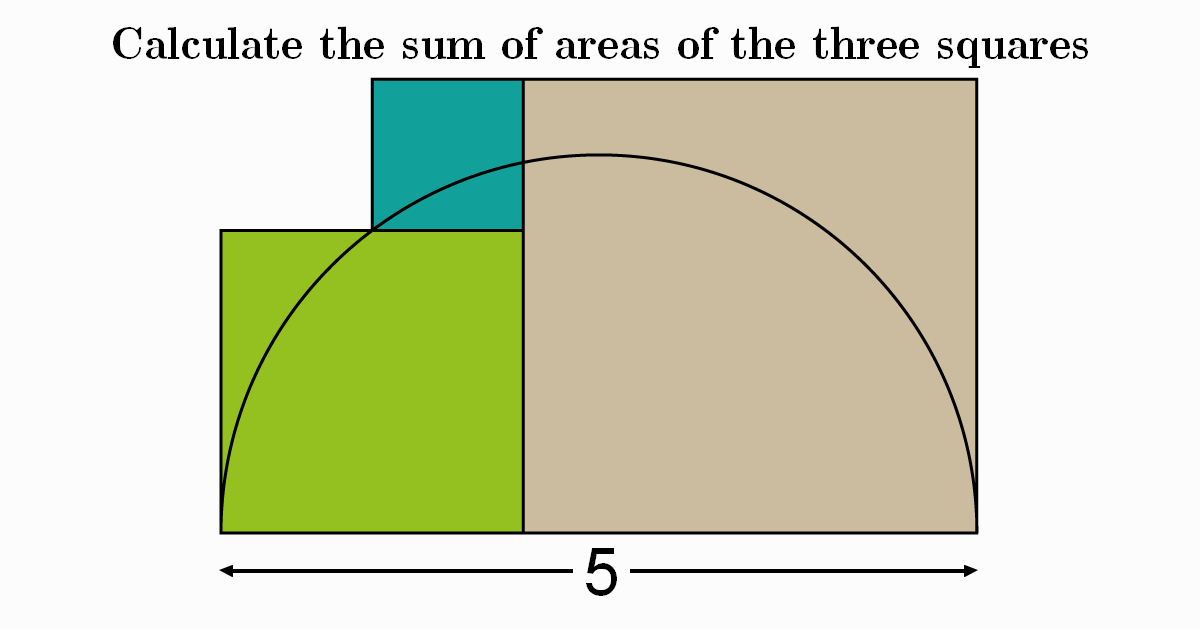
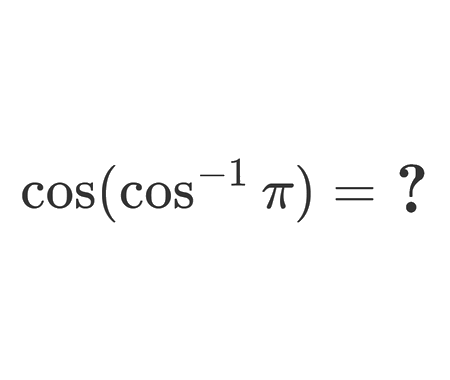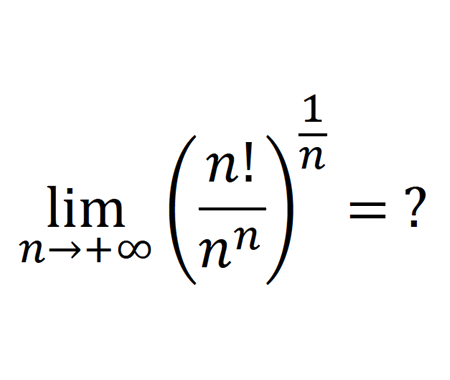Calculate the sum of areas of the three squares
Home -> Solved problems -> Areas three squares
Solution
We have a top part of a circle of diameter \(5\) drawn with three squares. To start let \(a\) be the side length of the blue square, and \(b\) the side length of the green square
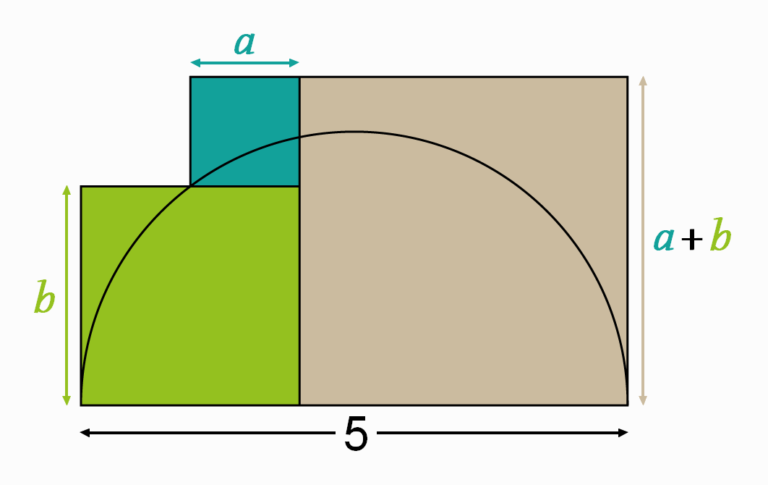
As we see in the previous figure the side of the grey square equals to \(a+b\). Let’s take the next example of similar right triangles
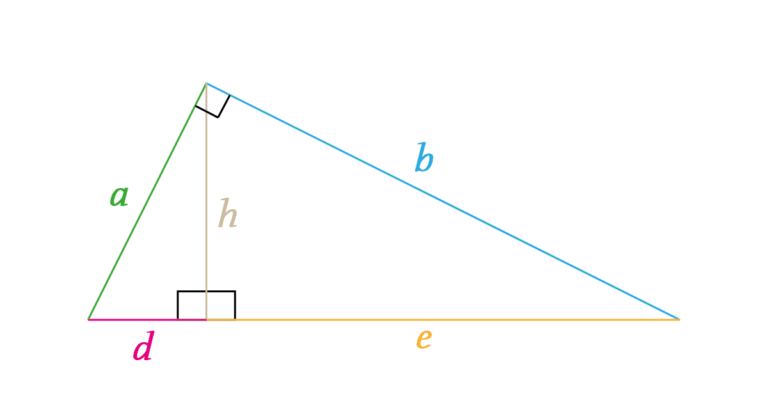
We get these results: \[a^{2}=d^{2}+h^{2}\] \[b^{2}=e^{2}+h^{2}\] \[\left(d+e\right)^{2}=a^{2}+b^{2}\] \[d^{2}+e^{2}+2de=a^{2}+b^{2}\] \[d^{2}+e^{2}+2de=d^{2}+h^{2}+e^{2}+h^{2}\] \[2de=2h^{2}\] \[h^{2}=de\]
Now let’s return to our problem and apply the previous result to the next figure
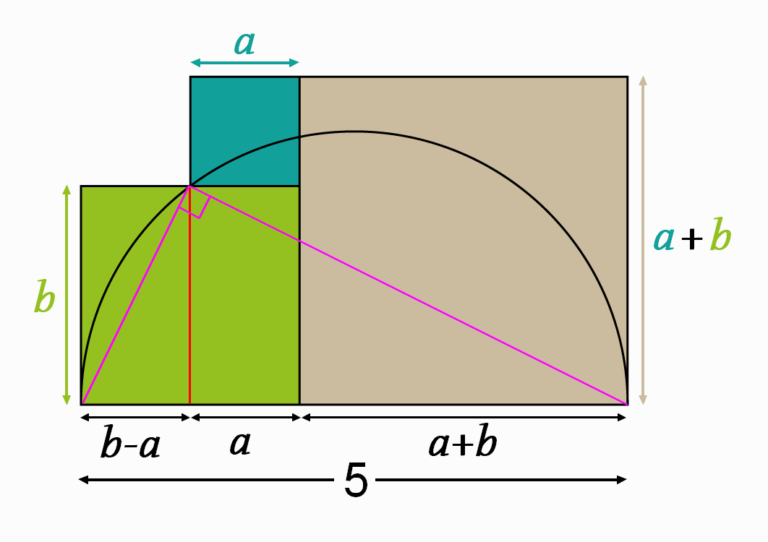
Therefore we get, \[b^{2}=\left(b-a\right)\left(2a+b\right)\] \[=2ab+b^{2}-2a^{2}-ab\] \[2a^{2}-ab=0\] \[a\left(2a-b\right)=0\] \[\color{blue} {a\neq0}\] \[\Rightarrow2a=b\] Using another fact in the figure, we have \[\left(b-a\right)+a+\left(a+b\right)=5\] \[2b+a=5\] \[2\left(2a\right)+a=5\] \[5a=5\] \[a=1\] Finally, let \(S\) be the sum of areas of the three squares, thus \[S=a^{2}+b^{2}+\left(a+b\right)^{2}\] \[=a^{2}+b^{2}+a^{2}+b^{2}+2ab\] \[=2a^{2}+2b^{2}+2ab\] \[=2\left(a^{2}+b^{2}+ab\right)\] \[=2\left(a^{2}+4a^{2}+2a^{2}\right)\] \[=14a^{2}\] \[\large \Rightarrow S=14\]
Home -> Solved problems -> Areas three squares
Every problem you tackle makes you smarter.
↓ Scroll down for more math problems↓
↓ ↓
↓ ↓
↓ ↓
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
Home -> Solved problems -> Areas three squares