Home -> Solved problems -> Find the value of the length x
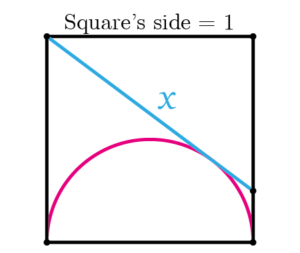
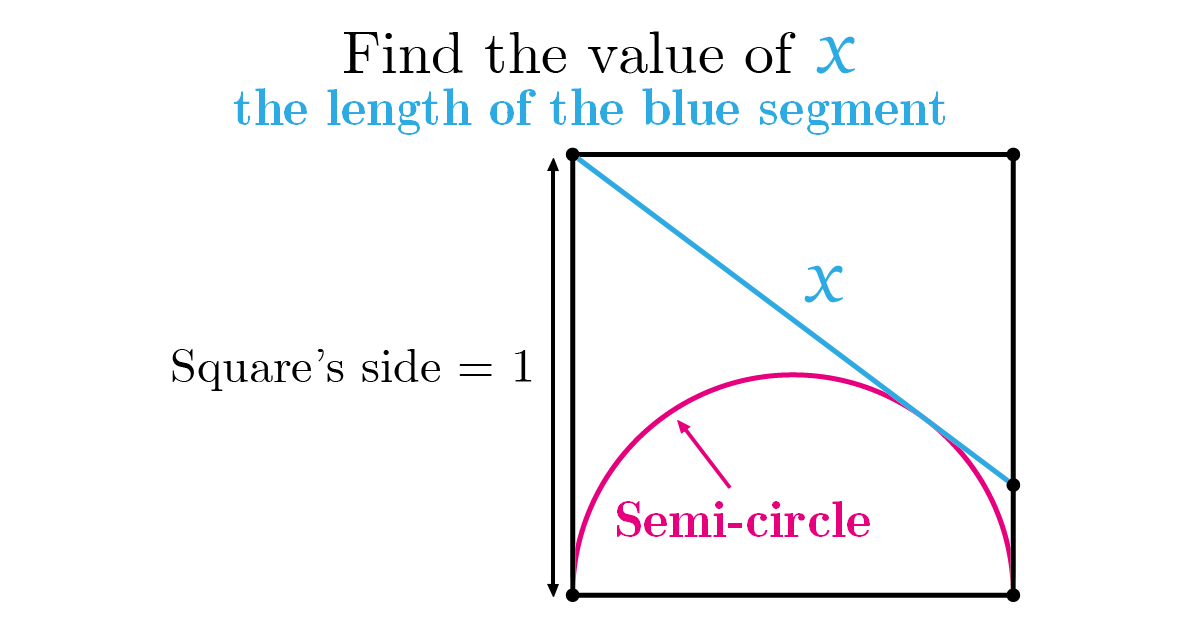
Find the value of the length \(x\)
Solution
Let’s recall that a pair of tangents from a point outside a circle have equal length. \(AB=AC\).
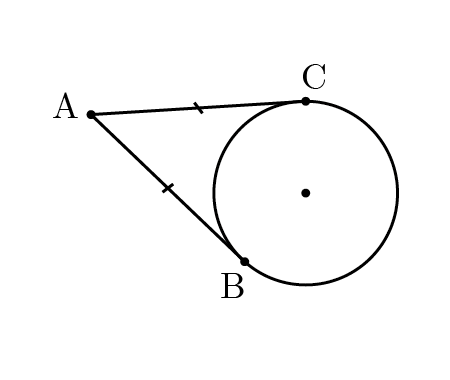
Applying the previous fact to our problem and knowing that the pink shape is a semi-circle, we get these results
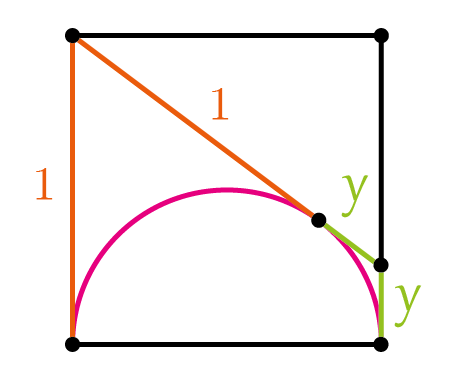
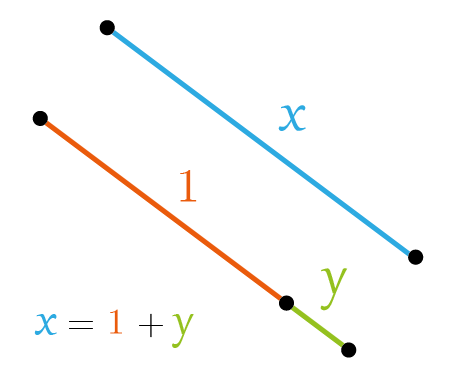
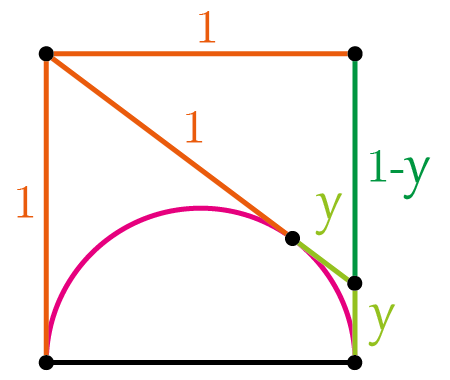
Now, we apply Pythagoras theorem to the next triangle
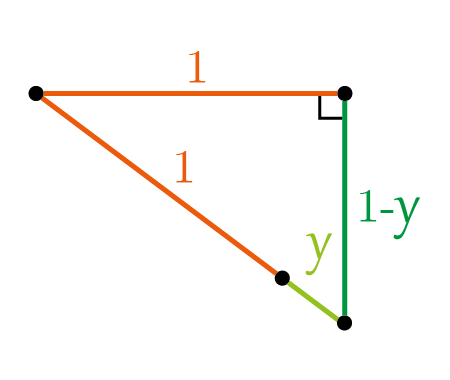
\[(1+y)^{2} =(1-y)^{2}+1^{2}\]
\[y^{2}+2 y+1 =y^{2}-2 y+1+1 \]
\[4 y =1\]
\[y =\frac{1}{4}\]
\[x =y+1 \]
\[=\frac{1}{4}+1 \]
\[=\frac{5}{4} \]
\[\huge x =\frac{5}{4}\]
Home -> Solved problems -> Find the value of the length x
Every problem you tackle makes you smarter.
↓ Scroll down for more math problems↓
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?
Home -> Solved problems -> Find the value of the length x
Share the solution: Find the value of the length \(x\)