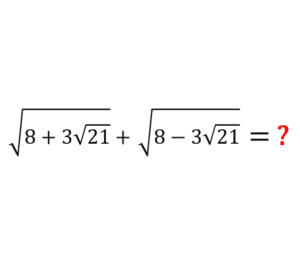Home -> Solved problems -> Cube roots and square roots expression
Find the value of the expression
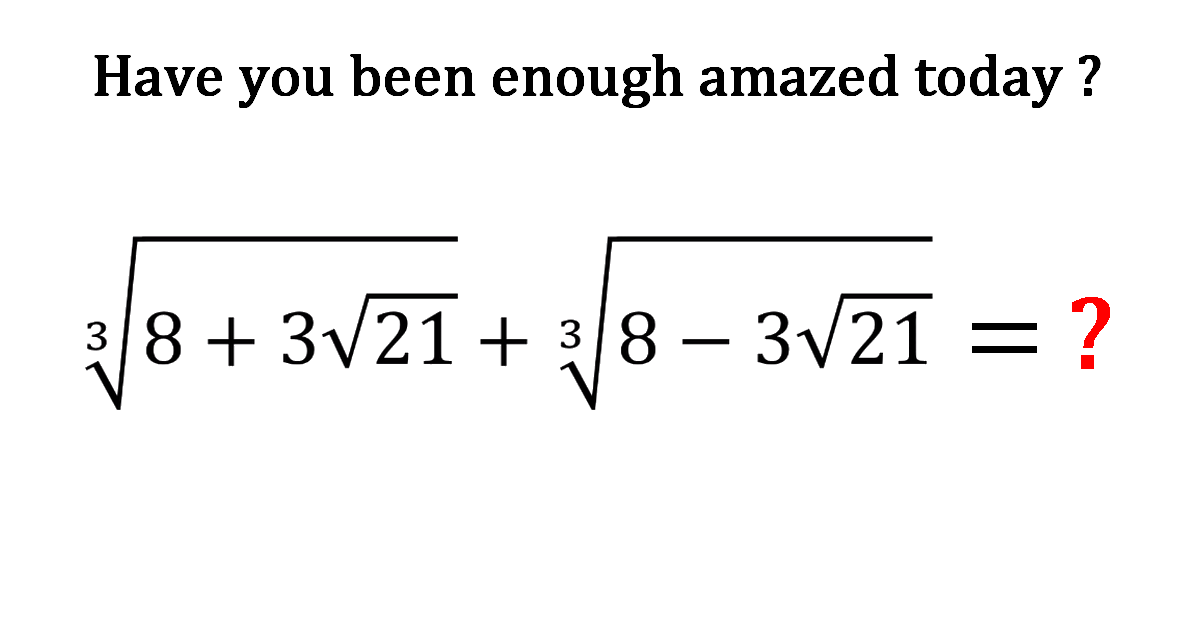
Solution
\[\begin{aligned}
&a=8+3 \sqrt{21} \\\\
&b=8-3 \sqrt{21}
\end{aligned}\]
\[\begin{aligned}
x&=\sqrt[3]{a}+\sqrt[3]{b}\\\\
x^{3}&=(\sqrt[3]{a}+\sqrt[3]{b})^{3} \\\\
&=a+b+3(\sqrt[3]{a})^{2}(\sqrt[3]{b})+3(\sqrt[3]{b})^{2}(\sqrt[3]{a})\\\\
&=a+b+3 \sqrt[3]{a a b}+3 \sqrt[3]{b b a} \\\\
a b&=b a =(8+3 \sqrt{21})(8-3 \sqrt{21}) \\\\
&=8^{2}-3^{2}(21) \\\\
&=-125=(-5)^{3}
\end{aligned}\]
\[\begin{aligned}
x^{3} &=a+b+3(-5) \sqrt[3]{a}+3(-5) \sqrt[3]{b} \\\\
&=a+b-15(\sqrt[3]{a}+\sqrt[3]{b})\\\\
x&=\sqrt[3]{a}+\sqrt[3]{b} \\\\
x^{3}&=16-15x\\\\
x^{3}&+15x-16=0
\end{aligned}\]
Notice \(x=1\) is a solution, Thus \((x-1)\) is a factor: \[(x-1)\left(x^{2}+x+16\right)=0\]
The quadratic roots involve imaginary parts and non-zero. We know that: \[\begin{array}{ll}
a=8+3 \sqrt{21} & \sqrt[3]{a} \in \mathbb{R} \\\\
b=8-3 \sqrt{21} & \sqrt[3]{b} \in \mathbb{R}
\end{array}\] \[\Rightarrow x=1\]
Therefore \[\large \sqrt[3]{8+3 \sqrt{21}}+\sqrt[3]{8-3 \sqrt{21}}=1\]
Home -> Solved problems -> Cube roots and square roots expression
Related Topics: Solved Problems
Home -> Solved problems -> Cube roots and square roots expression
Share the solution: Find the value of the expression