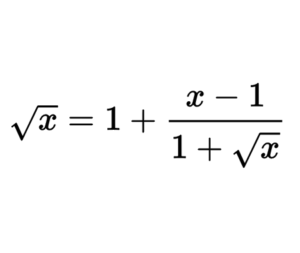Home -> Solved problems -> How many roots
How many real roots does the equation have?
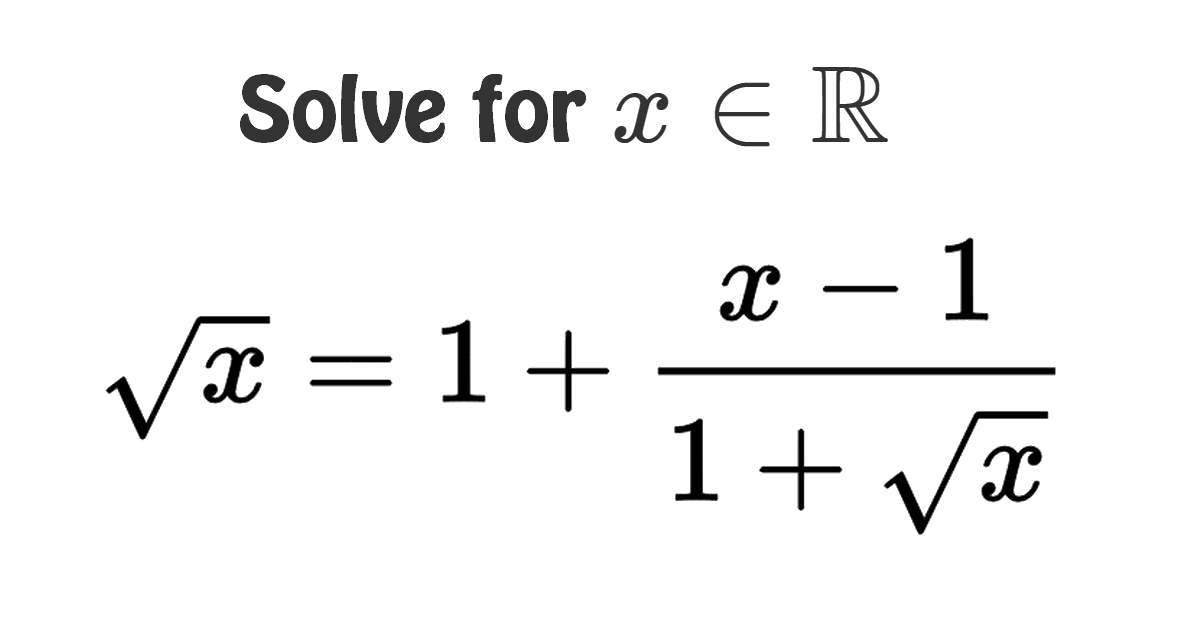
Solution
\[\sqrt{x}=1+\frac{x-1}{1+\sqrt{x}}\;\;\;\;\;\;\;(1)\] Let \(x\geq0\) and \(\sqrt{x}=t\), thus \[t=1+\frac{t^{2}-1}{1+t}\] \[t(1+t)=1+t+t^{2}-1\] \[t+t^{2}=1+t+t^{2}-1\] \[0=0\] Therefore, the equation \((1)\) is an identity if only \(x\geq0\) \[\huge S_{\mathbb{R}}=[0,+\infty[\]
Home -> Solved problems -> How many roots
Related Topics
Home -> Solved problems -> How many roots
Share the solution: How many roots ?