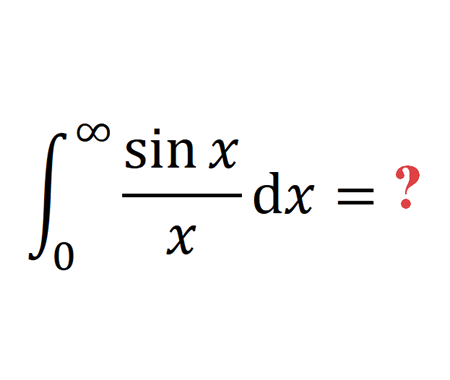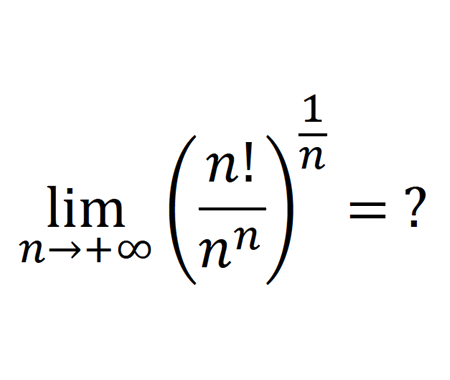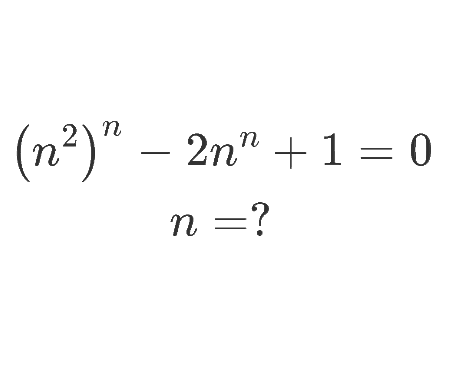Calculate the limit using geometric mean
Home -> Solved problems -> Limit geometric mean
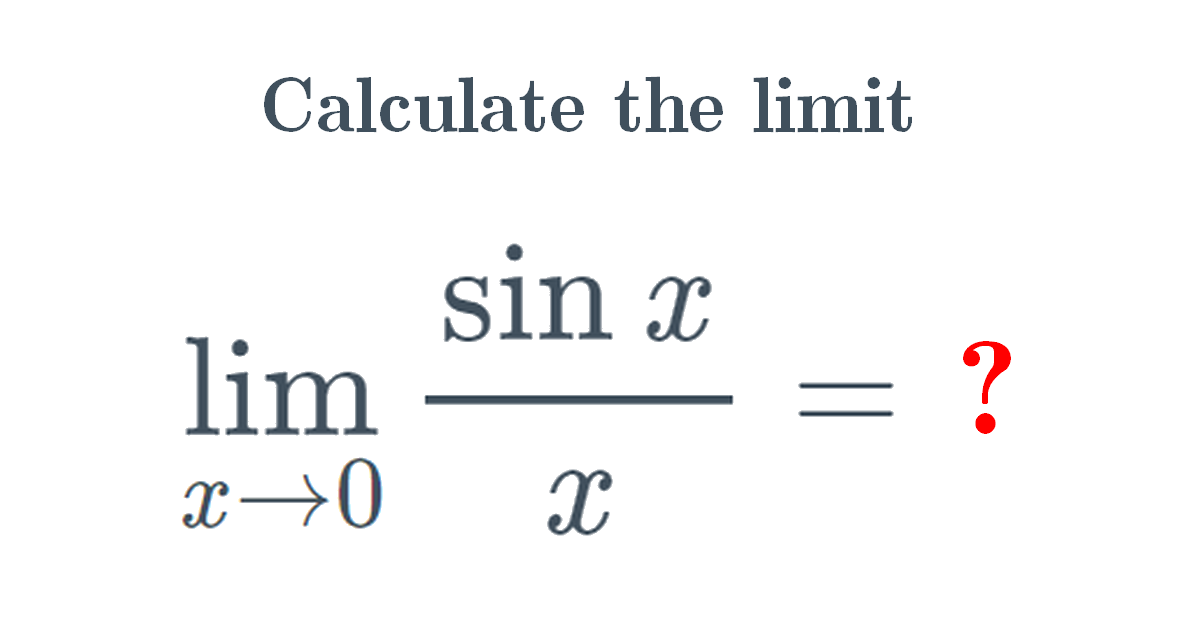
Solution
In the next figure we have a circle arc of radius 1 and center \(A\). Let \(S\) be the area of the triangle \(\triangle ABC\) thus, \[S=\frac{1}{2}AB\sin x=\frac{1}{2}\sin x\]
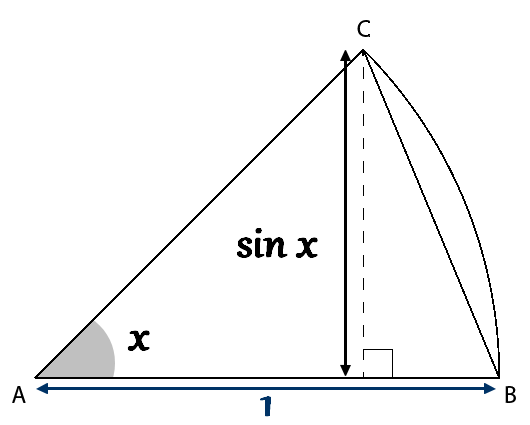
Let \(W\) be the area of the circular sector shaded in grey in the next figure, \[W=\frac{1}{2}x\] \(T\) is the area of the triangle \(\triangle ABD\)\[T=\frac{1}{2}ABDB=\frac{1}{2}\tan x\]
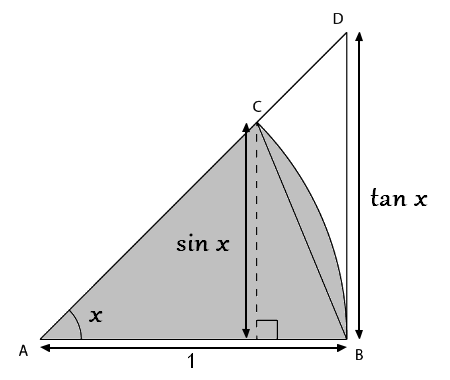
By inclusion, we have \(T\geq W\geq S\) thus, \[\frac{1}{2}\tan x\geq \frac{1}{2}x\geq \frac{1}{2}\sin x\] Dividing the previous inequality by \(\frac{1}{2}\sin x\) and taking reciprocals, we get \[\cos x\leq\frac{\sin x}{x}\leq1\] Since \(x\rightarrow\frac{\sin x}{x}\) and \(x\rightarrow\cos x\) are two even functions the inequality \(\cos x\leq\frac{\sin x}{x}\leq1\) is valid for any non-zero \(x\) between \(-\frac{\pi}{2}\) and \(-\frac{\pi}{2}\). Finally, knowing that \(\cos0=1\) and using squeeze theorem we get that \[\lim_{x \rightarrow 0}\frac{\sin x}{x}=1\]
Home -> Solved problems -> Limit geometric mean
Every problem you tackle makes you smarter.
↓ Scroll down for more maths problems↓
↓ ↓
↓ ↓
↓ ↓
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
Home -> Solved problems -> Limit geometric mean