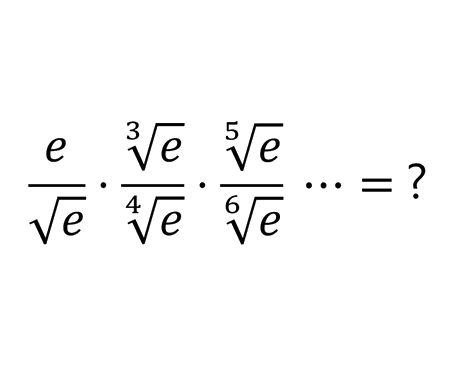Home -> Solved problems -> Infinite product
Infinite product
Solution
\[\begin{aligned}
P_{n} &=\frac{e}{\sqrt{e}} \cdot \frac{\sqrt[3]{e}}{\sqrt[4]{e}} \cdot \frac{\sqrt[5]{e}}{\sqrt[6]{e}} \cdots \frac{\sqrt[n-1]{e}}{\sqrt[n]{e}} \\\\
&=\frac{e^{1}}{e^{\frac{1}{2}}} \cdot \frac{e^{\frac{1}{3}}}{e^{\frac{1}{4}}} \cdot \frac{e^{\frac{1}{5}}}{e^{\frac{1}{6}}} \cdots \frac{e^{\frac{1}{n-1}}}{e^{\frac{1}{n}}}\\\\
&=e^{1}\cdot e^{-\frac{1}{2}}\cdot e^{\frac{1}{3}}\cdot e^{-\frac{1}{4}} \cdot e^{\frac{1}{5}}\cdot e^{-\frac{1}{6}}\cdots e^{\frac{1}{n-1}}\cdot e^{-\frac{1}{n}}\\\\
&=e^{1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\cdots+\frac{1}{n-1}-\frac{1}{n}}
\end{aligned}\]
\[\text { Maclaurin Series of } \ln (1+x) :\]
\[\begin{gathered}
\ln (1+x)=x-\frac{x^{2}}{2}+\frac{x^{3}}{3}+\cdots \\\\
-1<x\leq 1\\\\
For\; x=1\\\\
\ln (1+1)=1-\frac{1}{2}+\frac{1}{3}+\cdots\\\\
\ln (2)=1-\frac{1}{2}+\frac{1}{3}+\cdots
\end{gathered}\]
\[\begin{aligned}
\lim_{n \rightarrow \infty}P_{n} &=\lim_{n \rightarrow \infty}e^{1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\cdots+\frac{1}{n-1}-\frac{1}{n}}\\\\
&=e^{\lim_{n \rightarrow \infty}1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\cdots+\frac{1}{n-1}-\frac{1}{n}}\\\\
&=e^{\ln2}\\\\
&=2
\end{aligned}\]
\[\large \Rightarrow\frac{e}{\sqrt{e}} \cdot \frac{\sqrt[3]{e}}{\sqrt[4]{e}} \cdot \frac{\sqrt[5]{e}}{\sqrt[6]{e}}\cdots=2\]
Home -> Solved problems -> Infinite product
Every problem you tackle makes you smarter.
↓ Scroll down for more math problems↓
Home -> Solved problems -> Infinite product