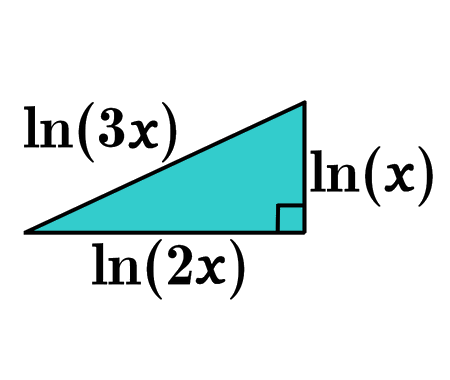Every problem you tackle makes you smarter.

↓ Scroll down for more maths problems↓

How Tall Is The Table ?

Solution

How far apart are the poles ?

Solution

Determine the square's side \(x\)

Solution

Find the volume of the interior of the kiln

Solution

Solve the equation for real values of \(x\)

Solution

Find the equation of the curve formed by a cable suspended between two points at the same height

Solution

Why 0.9999999...=1

Solution

Calculate the integral

Solution

Error to avoid that leads to:

Solution

What's the problem ?

Solution

Explain your answer without using calculator

Solution

Calculate the sum of areas of the three squares

Solution

What values of \(x\) satisfy this inequality

Solution

Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x} \) has a curvilinear asymptote \(y=x^{2}+2 x+3\)

Solution

Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?

Solution

Only one in 1000 can solve this math problem

Solution

Calculate the following

Solution

Find the limit of width and height ratio

Solution

Is \(\pi\) an irrational number ?

Solution

Solve for \(x \in \mathbb{R}\)

Solution

Prove that \(e\) is an irrational number

Solution

Prove that

Solution

Challenging problem

Solution

Solve the equation for \(x \in \mathbb{R}\)

Solution

Calculate the following limit

Solution

Calculate the following limit

Solution

Determine the angle \(x\)

Solution

Find the derivative of \(y\) with respect to \(x\)

Solution

Prove Wallis Product Using Integration

Solution

Calculate the radius R

Solution

Calculate the volume of Torus using cylindrical shells

Solution

Find the derivative of exponential \(x\) from first principles

Solution

Find the volume of the square pyramid as a function of \(a\) and \(H\) by slicing method.

Solution

Prove that \[\lim_{x \rightarrow 0}\frac{\sin x}{x}=1\]

Solution

Prove that

Solution

Calculate the half derivative of \(x\)

Solution

Find out what is a discriminant of a quadratic equation.

Solution

Calculate the rectangle's area

Solution

Infinitely nested radicals

Solution

Determine the square's side \(x\)

Solution

Wonderful math fact: 12542 x 11 = 137962

Explanation

Calculate the sum

Solution

What is the new distance between the two circles ?

Solution

Solve the equation for \(x\epsilon\mathbb{R}\)

Solution

Calculate the area of the Squid Game diagram blue part

Solution

Calculate the limit

Solution

Find the infinite sum

Solution

Calculate the integral

Solution

Prove that

Solution

Can we set up this tent ?

Solution

Find the value of \(h\)

Solution

Is the walk possible?

Solution

Find the length of the black segment

Solution

Prove that pi is less than 22/7

Solution

Find the value of \(x\)

Solution

Amazing !

Solution

Prove that

Solution

What is the weight of all animals ?

Solution

Determine the length \(x\) of the blue segment

Solution

if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?

Solution

What is the value of the following infinite product?

Solution

Which object weighs the same as the four squares?

Solution

What is \((-1)^{\pi}\) equal to?

Solution

Can you solve it?

Solution

Can you solve it?

Solution

Great Math Problem

Solution

Calculate the integral \(\int_{0}^{1}(-1)^{x} d x\)

Solution

Find the general term of the sequence

Solution

Find the radius of the blue circles

Solution

Determine the area of the green square

Solution

Find the area of the square

Solution

Calculate the integral

Solution

Calculate the integral

Solution

Calculate

Solution

What is the radius of the smallest circle ?

Solution

Find the Cartesian equation of the surface

Solution

Calculate the integral

Solution

Calculate the limit

Solution

Can you solve this ?

Solution

Solve the quintic equation for real \(x\)

Solution

How many students study no language ?

Solution

Probability of seeing a car in 10 minutes

Solution

What is the number of where the car stands ?

Solution

What is the value of \(x\) ?

Solution

Prove that

Solution

Is it possible to solve for \(x\) so that \(ln(x)\), \(ln(2x)\), and \(ln(3x)\) form a right triangle?

Solution

How many times will circle A revolve around itself in total ?

Solution

Find the distance \(BC\)

Solution

Solve for a^6, a : positive number

Solution

Solve the quadratic equation by Completing the Square

Solution

Determine the length and width of the rectangular region of the house

Solution