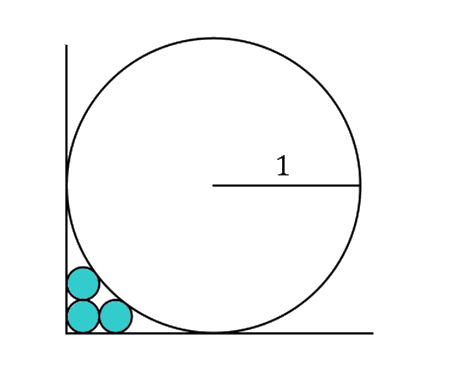Calculate the half derivative of \(x\)
Home -> Solved problems -> Half derivative of x
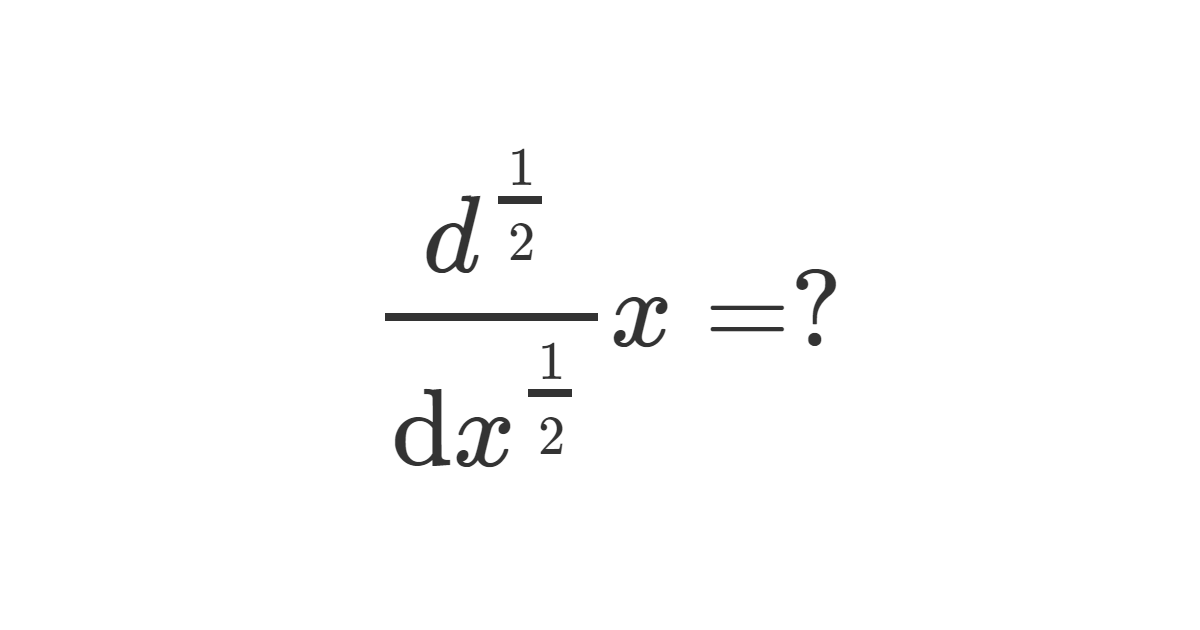
Solution
Let the function \[f\left(x\right)=x^{k}\Rightarrow f’\left(x\right)=\frac{\text{d}}{\text{d}x}f\left(x\right)=kx^{k-1}\] The general result is: \[\frac{d^{a}}{dx^{a}}x^{k}=\frac{k!}{(k-a)!}x^{k-a}\] Now let’s use the Gamma function instead of factorials, we get \[\frac{d^{a}}{dx^{a}}x^{k}=\frac{\gamma\left(k+1\right)}{\gamma\left(k-a+1\right)}x^{k-a}\;\;\;\;\;\;\;k\geq0\] For \(k=1\) and \(a=\frac{1}{2}\), we obtain the half derivative of the function \(x\rightarrow x\) \[\frac{d^{\frac{1}{2}}}{dx^{\frac{1}{2}}}x=\frac{\gamma\left(1+1\right)}{\gamma\left(1-\frac{1}{2}+1\right)}x^{1-\frac{1}{2}}=\frac{\gamma\left(2\right)}{\gamma\left(\frac{3}{2}\right)}x^{\frac{1}{2}}=\frac{1}{\frac{\sqrt{\pi}}{2}}x^{\frac{1}{2}}\] Therefore \[\color{black} {\large \frac{d^{\frac{1}{2}}}{dx^{\frac{1}{2}}}x=\frac{2x^{\frac{1}{2}}}{\sqrt{\pi}}}\] To demonstrate that this is in fact the half derivative we repeat the process: \[\frac{d^{\frac{1}{2}}}{dx^{\frac{1}{2}}}\frac{2x^{\frac{1}{2}}}{\sqrt{\pi}}=\frac{2}{\sqrt{\pi}}\frac{\gamma\left(1+\frac{1}{2}\right)}{\gamma\left(\frac{1}{2}-\frac{1}{2}+1\right)}x^{\frac{1}{2}-\frac{1}{2}}=\frac{2}{\sqrt{\pi}}\frac{\gamma\left(\frac{3}{2}\right)}{\gamma\left(1\right)}x^{0}=\frac{2\frac{\sqrt{\pi}}{2}x^{0}}{\sqrt{\pi}}=1\] (because \(\gamma\left(\frac{3}{2}\right)=\frac{1}{2}\sqrt{\pi}\) and \(\gamma\left(1\right)=1\)) \[\Rightarrow\left(\frac{d^{\frac{1}{2}}}{dx^{\frac{1}{2}}}\frac{d^{\frac{1}{2}}}{dx^{\frac{1}{2}}}\right)x=\frac{d}{dx}x=1\]
Home -> Solved problems -> Half derivative of x
Every problem you tackle makes you smarter.
↓ Scroll down for more maths problems↓
↓ ↓
↓ ↓
↓ ↓
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
Home -> Solved problems -> Half derivative of x