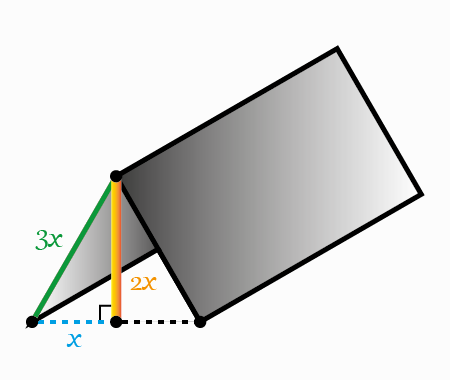
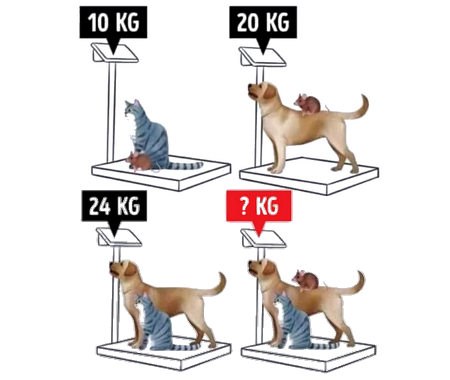
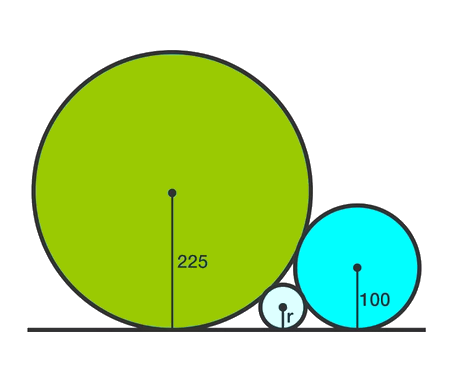
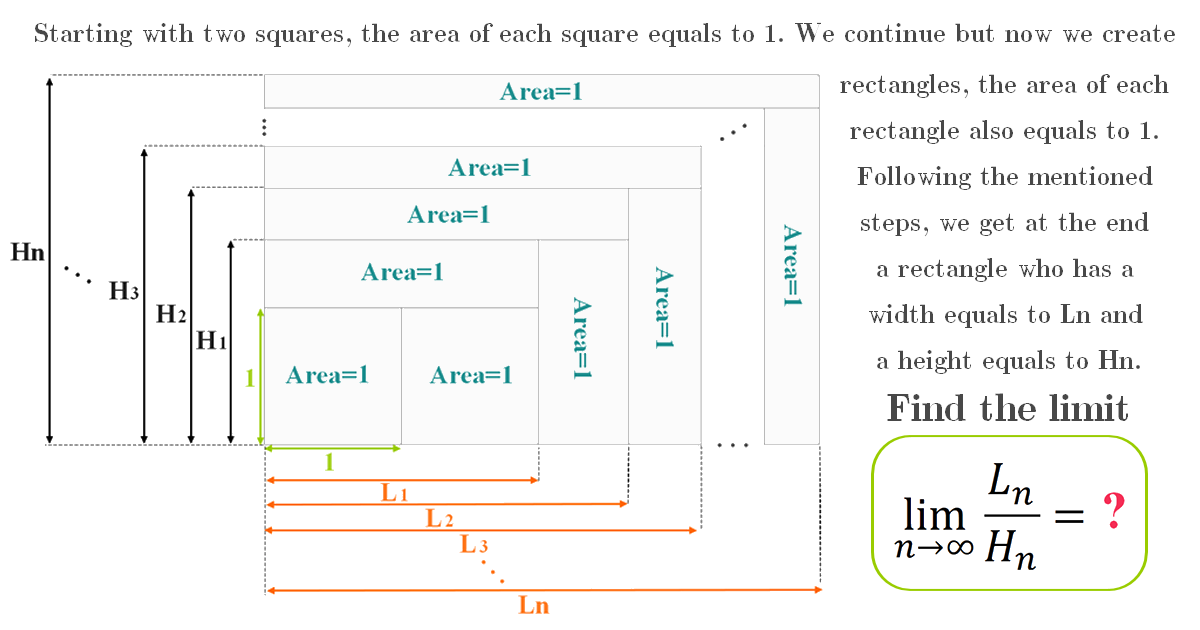
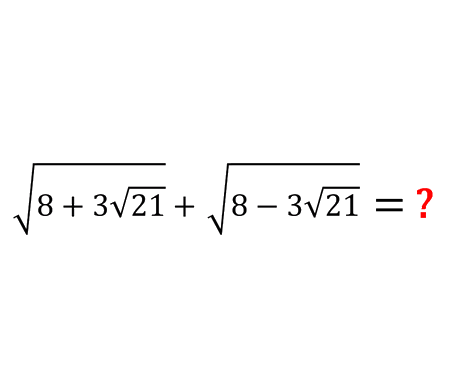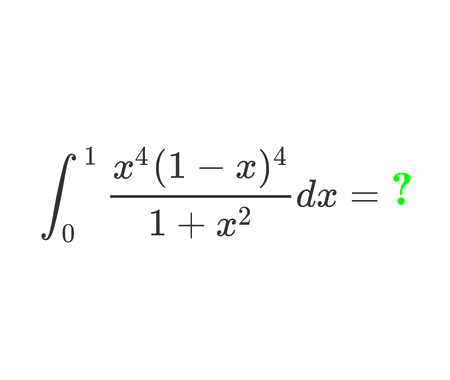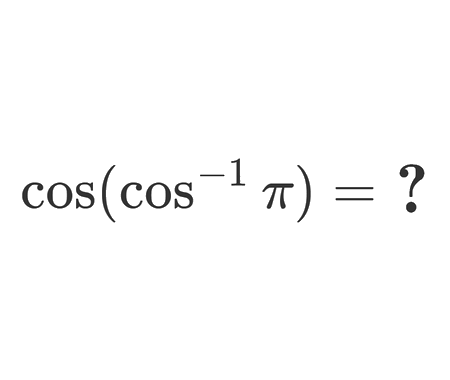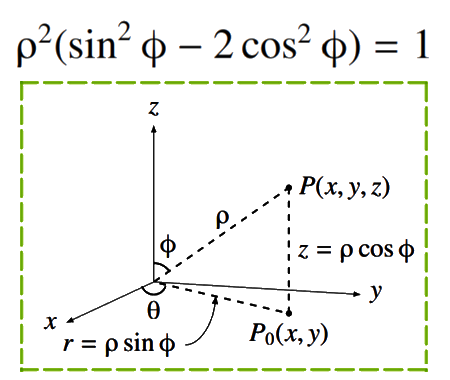Find the limit of width and height ratio
Home -> Solved problems -> Find the limit of width and height ratio
Solution
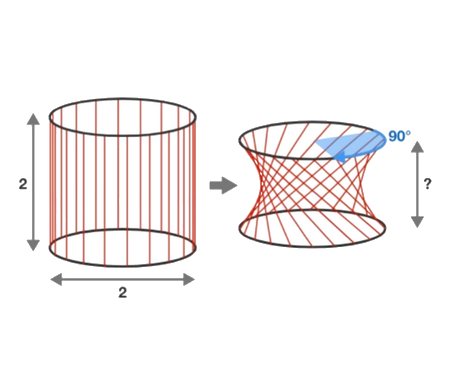
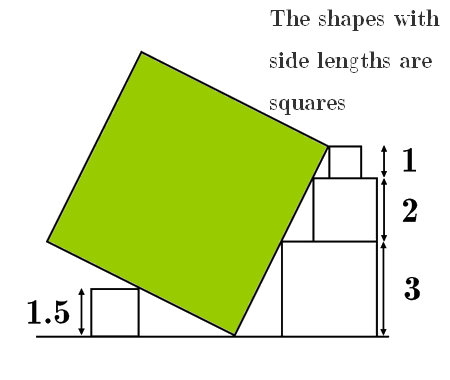
For the geometric construction, we have \(L_{0} H_{0}=1, L_{1} H_{0}=2, L_{1} H_{1}=3\) so more in general \(L_{i} H_{j}=1+i+j\). Around the nth step the equations are \[\left\{\begin{array}{c}
L_{n} H_{n-1}=2 n \\
L_{n} H_{n}=2 n+1 \\
L_{n+1} H_{n}=2 n+2
\end{array}\right.\]
Two recurrence sequences can be obtained by dividing the second equation with the first one and the third equation with the second one \[\left\{\begin{array} { c }
{ H _ { 0 } = 1 } \\
{ H _ { n } = H _ { n – 1 } \frac { 2 n + 1 } { 2 n } }
\end{array} \quad \left\{\begin{array}{c}
L_{0}=1 \\
L_{n}=L_{n-1} \frac{2 n+2}{2 n+1}
\end{array}\right.\right.\] Explaining each recurrence sequence \[H_{n}=\frac{2 n+1}{2 n} H_{n-1}\] \[=\frac{2 n+1}{2 n} \frac{2 n-1}{2 n-2} H_{n-2}\] \[\vdots\] \[=\frac{(2 n+1)(2 n+1) \cdots 3}{2 n(2 n-2) \cdots 2} H_{0}\] \[=\prod_{k=1}^{n} \frac{2 k+1}{2 k}\] \[=\frac{(2 n+1) ! !}{2^{n} n !}\] \[=\frac{(2 n+1)(2 n) !}{4^{n}(n !)^{2}}\] \[L_{n}=\frac{2 n}{2 n-1} L_{n-1}\] \[=\frac{2 n}{2 n-1} \frac{2 n-2}{2 n-3} L_{n-2}\] \[\vdots\] \[=\frac{2 n(2 n-2) \cdots 2}{(2 n-1)(2 n-3) \cdots 1} L_{0}\] \[=\prod_{k=1}^{n} \frac{2 k}{2 k-1}\] \[=\frac{2^{n} n !}{(2 n-1) ! !}\] \[=\frac{4^{n}(n !)^{2}}{(2 n) !}\]
So \[\lim _{n \rightarrow \infty} \frac{L_{n}}{H_{n}}=\lim _{n \rightarrow \infty} \frac{16^{n}(n !)^{4}}{[(2 n) !]^{2}(2 n+1)}\]
\[\text { Using Stirling’s formula }\] \[\left(n ! \approx n^{n} e^{-n} \sqrt{2 \pi n} \text { if } n\right. \text { goes to infinity) }\] \[(n !)^{4}=n^{4 n} e^{-4 n} 4 \pi^{2} n^{2} \] \[\quad[(2 n) !]^{2}=\left[(2 n)^{2 n} e^{-2 n} \sqrt{4 \pi n}\right]^{2}=16^{n} e^{-4 n} 4 \pi n\]
\[\large \lim _{n \rightarrow \infty} \frac{L_{n}}{H_{n}}=\lim _{n \rightarrow \infty} \frac{\pi n}{2 n+1}=\frac{\pi}{2}\]
Credit: Giuseppe Palaia
Home -> Solved problems -> Find the limit of width and height ratio
Every problem you tackle makes you smarter.
↓ Scroll down for more maths problems↓
↓ ↓
↓ ↓
↓ ↓
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
Home -> Solved problems -> Find the limit of width and height ratio