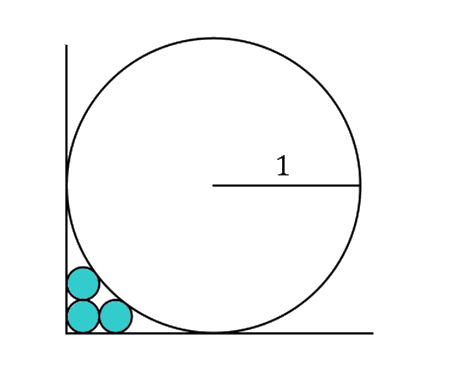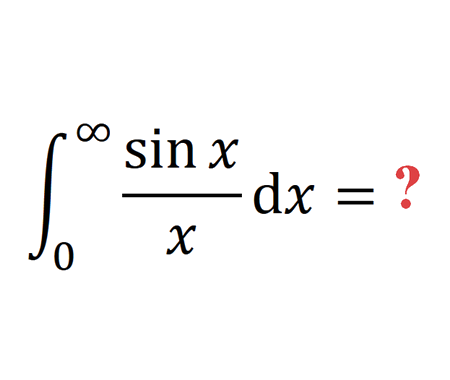Home -> Solved problems -> Calculate the integral
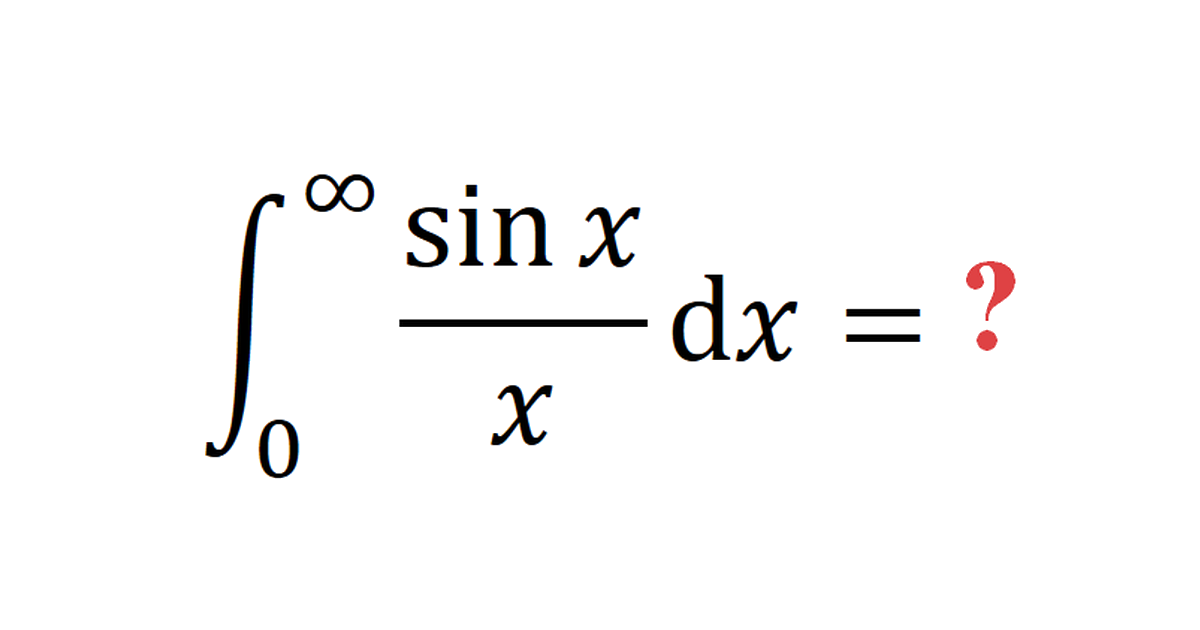
Solution
The convergence of the improper integral \(\int_{0}^{\infty} \frac{\sin (t)}{t} d t\) is classic : There is no problem at the origin because \(t \mapsto \sin (t) / t\) is extendable
by continuity, the only problem is therefore in \(\infty\). integrable on \([0,1]\), it is sufficient to ensure convergence on \([1,+\infty[:\) let \(x>1\), an integration by parts gives
\(
\int_{1}^{x} \frac{\sin (t)}{t} d t=\left[-\frac{\cos (t)}{t}\right]_{1}^{x}-\int_{0}^{x} \frac{\cos (t)}{t^{2}} d t
\)
when \(x\) approaches \(+\infty\) the term \(«\) in brackets \(»\) approaches \(\sin (1)\) and the second (since \(\left|\cos (t) / t^{2}\right| \leq t^{-2} \in L^{1}\left([1,+\infty[))\right.\) toward \(\int_{1}^{\infty} \cos (t) / t^{2} d t \in \mathbb{R}\). Therefore \(\int_{0}^{+\infty} \frac{\sin (t)}{t} d t\) converges.
Let
\[I(b)=\int_{0}^{\infty} \frac{\sin x}{x} e^{-b x} d x\;\;\;\;\;\;\;(1)\]
\[I(0)=\int_{0}^{\infty} \frac{\sin x}{x} \cdot e^{-0 x} d x\]
\[=\int_{0}^{\infty} \frac{\sin (x)}{x} d x\;\;\;\;\;\;\;(2)\]
Now,
\[I(b)=\int_{0}^{\infty} \frac{\sin x}{x} e^{-b x} d x\]
Differentiate resp \(b\) :
\[\begin{aligned}
I^{\prime}(b) &=\int_{0}^{\infty} \frac{d}{d b}\left(\frac{\sin (x)}{x} e^{-b x}\right) d x \\\\
I^{\prime}(b) &=\int_{0}^{\infty}-\frac{x \sin (x)}{x} e^{-b x} d x \\\\
I^{\prime}(b) &=-\int_{0}^{\infty} \sin (x) e^{-b x} d x .
\end{aligned}\]
Integrating by parts
\[I^{\prime}(b)=-\left[\frac{-e^{-b x}(\cos x+b \sin x)}{b^{2}+1}\right]_{x=0}^{x=\infty}\]
Applying limits
\[\begin{aligned}
I^{\prime}(b) &=0- \frac{e^{-b 0}(\cos 0+b \sin 0)}{b^{2}+1}\\\\
I^{\prime}(b) &=\frac{-1}{b^{2}+1}
\end{aligned}\]
Integrating resp \(b\), we get :
\[\begin{aligned}
&\int I^{\prime}(b) d b=\int-\frac{1}{b^{2}+1} d b \\\\
&I(b)=-\tan ^{-1}(b)+c=\int_{0}^{\infty} \frac{\sin x\; e^{-b x}}{x} d x\;\;\;\;\;\;from\;(1)
\end{aligned}\]
\[\begin{aligned}
&\text { Let } b \rightarrow \infty \\\\
&-\tan ^{-1}(\infty)+c=\int_{0}^{\infty} \frac{\sin x}{x} e^{-\infty .x} d x \\\\
&\frac{-\pi}{2}+c=0 \Rightarrow c=\pi / 2 \\\\
&\therefore I(b)=-\tan ^{-1}(b)+\pi / 2 \\\\
&I(0)=-\tan ^{-1}(0)+\pi / 2 \Rightarrow I(0)=\pi / 2 \\\\
&\text { From (2), } I(0)=\int_{0}^{\infty} \frac{\sin x}{x} d x=\frac{\pi}{2}
\end{aligned}\]
Home -> Solved problems -> Calculate the integral
Every problem you tackle makes you smarter.
↓ Scroll down for more maths problems↓
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?
Home -> Solved problems -> Calculate the integral