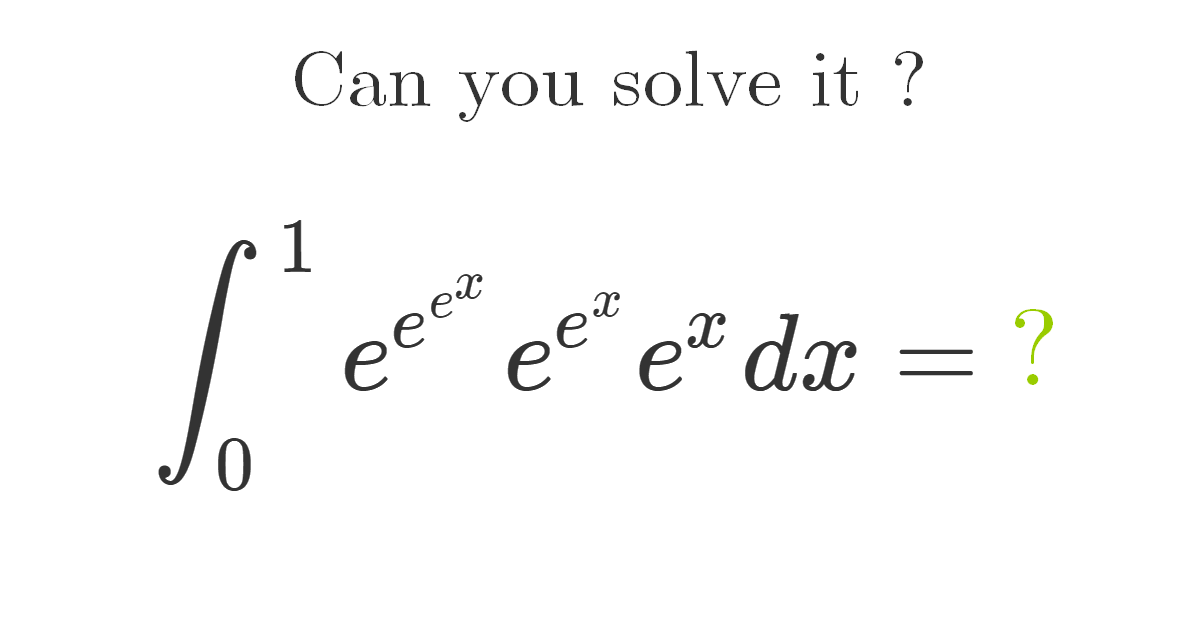
Solution
Introduction
In this problem, we explore the evaluation of the following integral:
$$ \int_{0}^{1} e^{\,e^{\,e^{x}}}\; e^{\,e^{x}}\; e^{x}\; dx $$
This expression involves a triple exponential function, which makes it look quite complicated at first glance. However, by recognizing patterns within nested exponentials, we can simplify the reasoning and find an elegant way to compute it. Such exercises demonstrate how composition of functions and differentiation rules can make even advanced integrals approachable.
Conclusion
This integral is a good example of how recognizing structure can greatly simplify complex expressions. Rather than relying on brute-force techniques, the solution reveals how understanding the relationship between a function and its derivative allows for a direct and elegant computation. This approach highlights one of the most beautiful aspects of calculus — finding simplicity hidden within layers of complexity.
Share the solution on facebook from here :
Every problem you tackle makes you smarter.
↓ Scroll down for more maths problems↓
