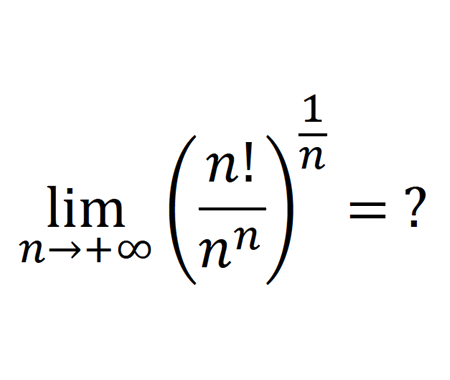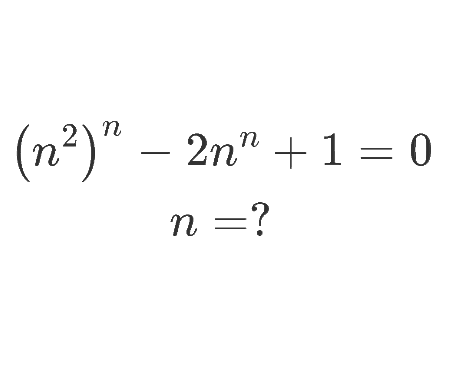How Tall Is The Table ?
Home -> Solved problems -> How tall is the table?
Solution
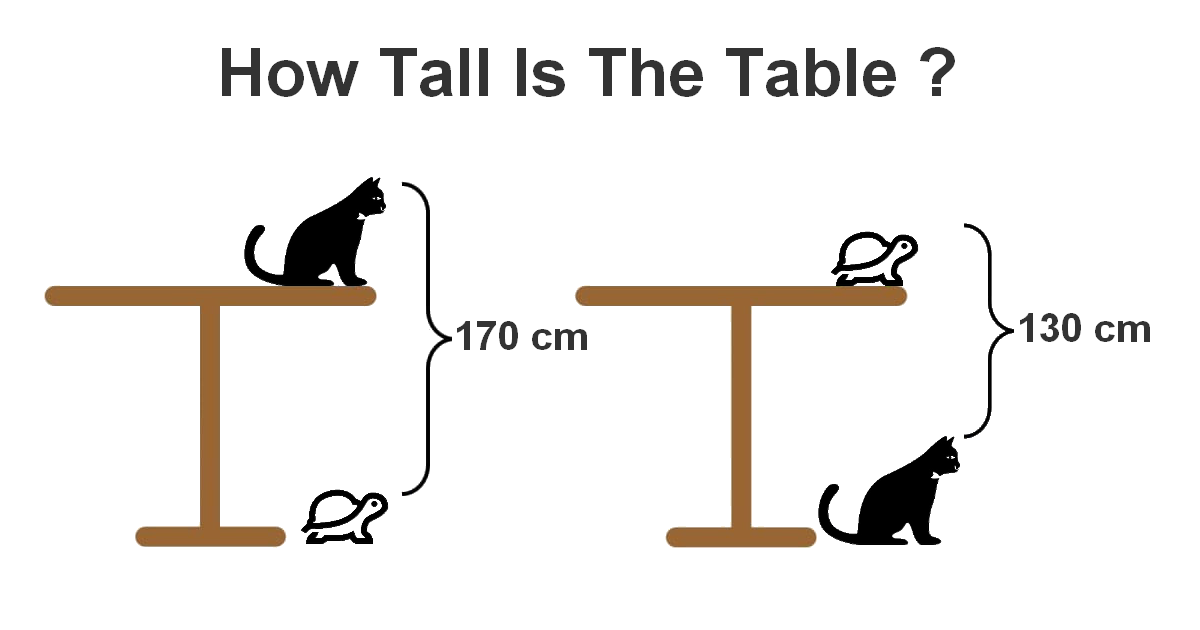
This visual math puzzle explores the famous problem “How tall is the table?”, where geometry and logical reasoning combine to reveal a surprising answer. By comparing the positions of hanging and lying objects, we can determine the exact height of the table without direct measurement.
Follow each step carefully — it’s an elegant demonstration of how proportion, symmetry, and visual deduction can solve what seems at first an impossible question.
Let: C be the height of the cat, T the height of the table and t the height of the turtle.
C + T – t = 170 (1)
t + T – C = 130 (2)
(1)+(2): 2T = 300
T = 150
Through this clever reasoning, we’ve shown that geometry often hides beauty in simplicity. The “How tall is the table?” puzzle reminds us that mathematics is not only about numbers, but about insight and perspective.
If you enjoyed this visual explanation, check out our Solved Exercises page for more fascinating proofs and creative problem-solving ideas.
Home -> Solved problems -> How tall is the table?
Every problem you tackle makes you smarter.
↓ Scroll down for more math problems↓
↓ ↓
↓ ↓
↓ ↓
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
Home -> Solved problems -> How tall is the table?