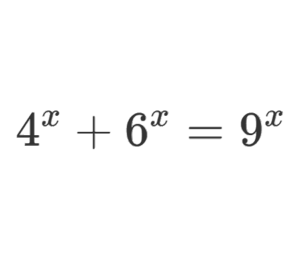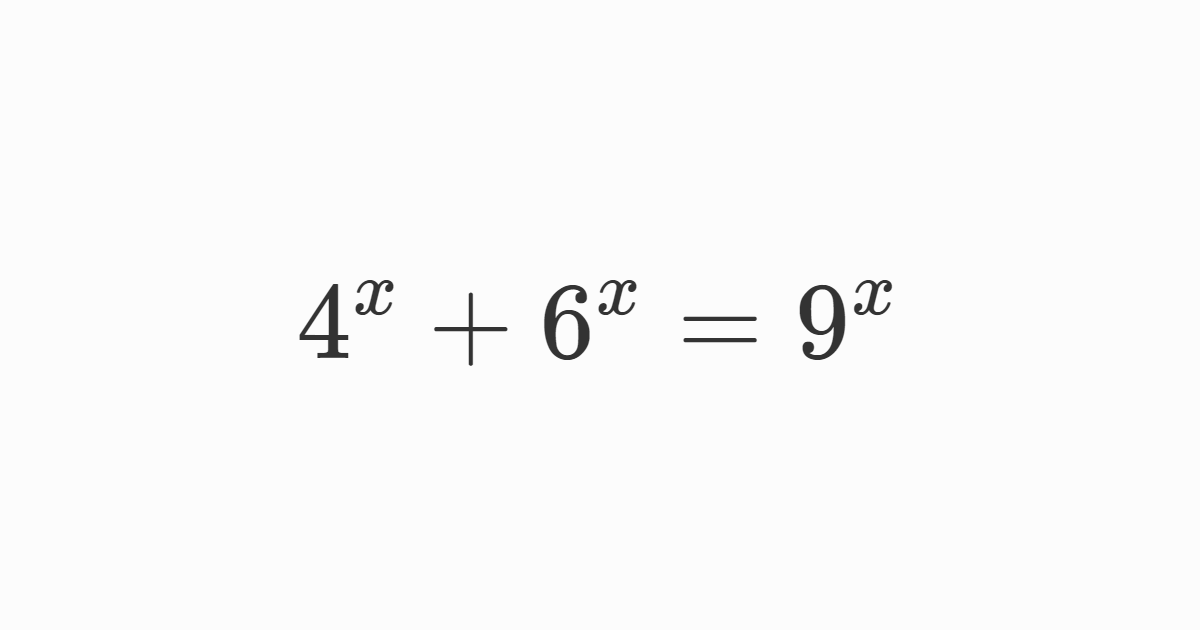We are dealing with an equation with numbers to the power of \(x\). Let’s start by dividing all the terms by \(4^{x}\), we get \[\frac{4^{x}}{4^{x}}+\frac{6^{x}}{4^{x}}=\frac{9^{x}}{4^{x}}\] \[\Rightarrow1+\left(\frac{6}{4}\right)^{x}=\left(\frac{9}{4}\right)^{x}\] \[\Rightarrow1+\left(\frac{3}{2}\right)^{x}=\left(\left(\frac{3}{2}\right)^{2}\right)^{x}\] \[\Rightarrow1+\left(\frac{3}{2}\right)^{x}=\left(\frac{3}{2}\right)^{2x}\] To continue, we make a change of variables. Let \(u=\left(\frac{3}{2}\right)^{x}\) thus \(\left(\frac{3}{2}\right)^{2x}=u^{2}\) \[\] Now after making the changes, we get a quadratic equation of form \[u^{2}=1+u\] \[\Rightarrow u^{2}-u-1=0\] We calculate the discriminant \(\delta \) \[\delta=\left(-1\right)^{2}-4\left(1\right)\left(-1\right)\] \[=1+4\] \[=5\] \[u=\frac{-\left(-1\right)-\sqrt{5}}{2\left(1\right)}\] \[=\frac{1-\sqrt{5}}{2}\] \[\color{red} {Or}\] \[u=\frac{-\left(-1\right)+\sqrt{5}}{2\left(1\right)}\] \[=\frac{1+\sqrt{5}}{2}\] \[u=\left(\frac{3}{2}\right)^{x}>0\] Therefore the solution \(u=\frac{1-\sqrt{5}}{2}\) is to be rejected. \[\Rightarrow u=\frac{1+\sqrt{5}}{2}\] \[\log u=\log\left(\left(\frac{3}{2}\right)^{x}\right)\] \[=x\log\left(\frac{3}{2}\right)\] \[\Rightarrow x=\frac{\log u}{\log\left(\frac{3}{2}\right)}\] \[\Rightarrow x=\frac{\log \left(\frac{1+\sqrt{5}}{2}\right)}{\log\left(\frac{3}{2}\right)}\approx1.19\]