Home -> Solved problems -> Catenary problem
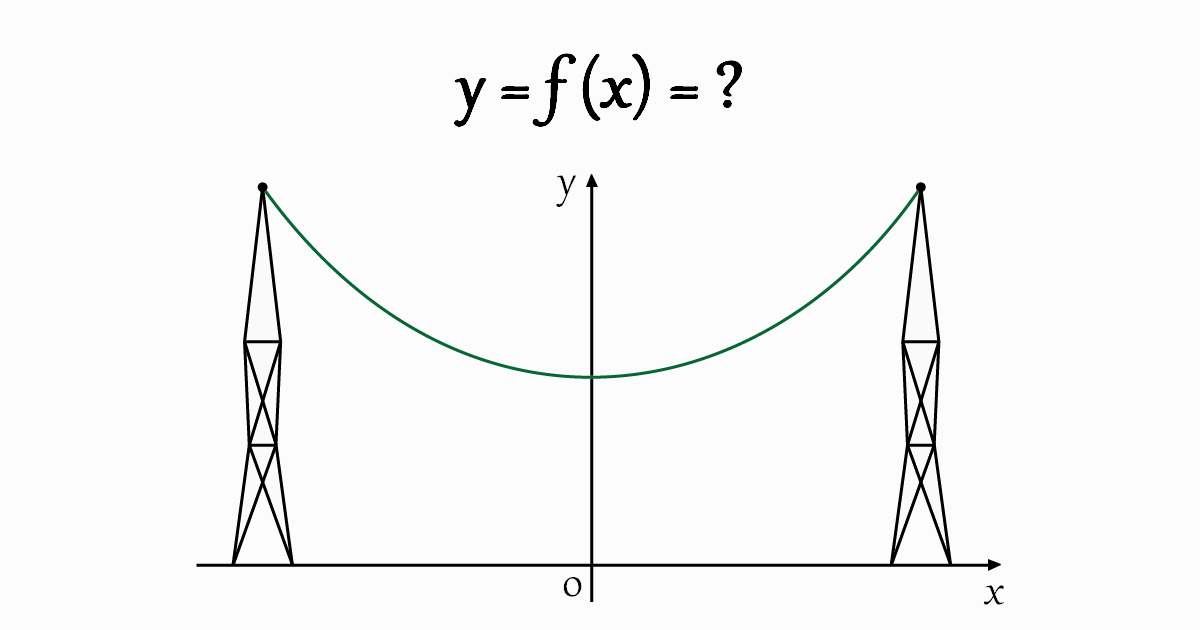
Find the equation of the curve formed by a cable suspended between two points at the same height.
Solution
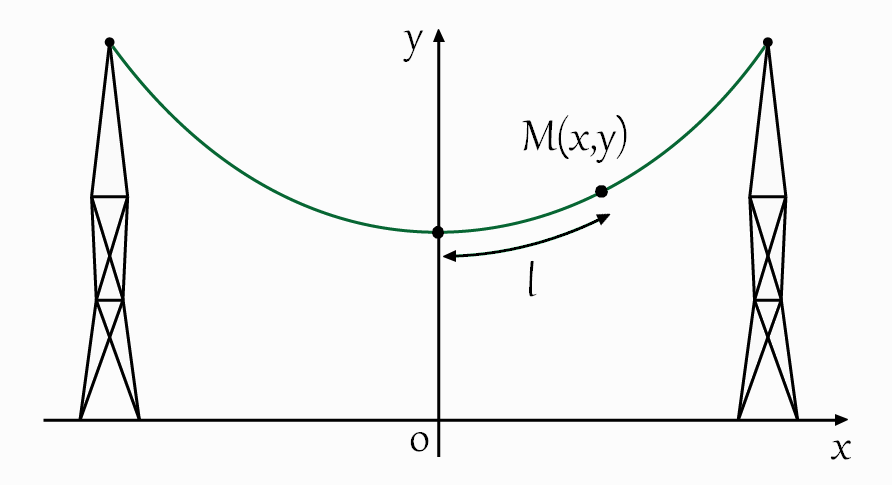
The heavy flexible cable takes a shape of a curve known as a catenary curve. As it is shown in the figure above, the cable is supported only at its ends. To start, let’s take an arbitrary point \(M\left(x,y\right)\) on the curve and let \(l\) be the length along the arc of the curve from the lowest point to \(M\).
Let \(w_{0}\) be the linear density of the deformed cable, it is its weight per unit length. The section between the lowest point and \(M\) is in static equilibrium under the impact of three forces. We have two tangent tensile forces and the weight which is divided to weights along the arc of the curve as it is shown in the next figure.
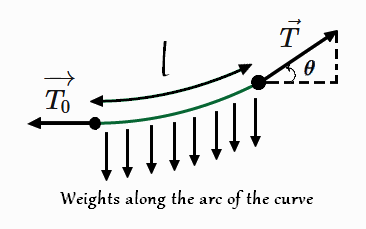
From the previous figure we have \[\tan\theta=\frac{\text{d}y}{\text{d}x}\] because \(\tan\theta\) is the slope of the tangent to curve at the point \(M\left(x,y\right)\). \[\] The condition for the static equilibrium indicates that \[\sum F_{x}=0\Rightarrow T_{0}=T\cos\theta\] We have an uniform distribution of weights therefore the global weight is equal to \(w_{0}l\) \[\sum F_{y}=0\Rightarrow w_{0}l=T\sin\theta\] From the two previous results calculated using the static equilibrium condition, we get \[\frac{w_{0}l}{T_{0}}=\tan\theta=\frac{\text{d}y}{\text{d}x}\] Let \(a=\frac{w_{0}}{T_{0}}\), \[\Rightarrow\frac{\text{d}y}{\text{d}x}=al\] Recall: The length of a curve arc can be found by \[\color{orange} {l=\int_{}^{} \sqrt{1+\left(\frac{\text{d}y}{\text{d}x}\right)^{2}}\text{d}x}\] \[\Rightarrow\frac{\text{d}l}{\text{d}x}= \sqrt{1+\left(\frac{\text{d}y}{\text{d}x}\right)^{2}}\] We have, \[\frac{\text{d}}{\text{d}x}\left(\frac{\text{d}y}{\text{d}x}\right)= \frac{\text{d}}{\text{d}x}\left(al\right)\] \[\frac{d^{2}y}{dx^{2}}=a\frac{\text{d}l}{\text{d}x}=a\sqrt{1+\left(\frac{\text{d}y}{\text{d}x}\right)^{2}}\] Let \[P=\frac{\text{d}y}{\text{d}x}\] \[\Rightarrow \frac{\text{d}P}{\text{d}x}=a\sqrt{1+P^{2}}\] \[\Rightarrow \frac{1}{\sqrt{1+P^{2}}}\text{d}P=a\text{d}x\] Thus, \[\int_{}^{} \frac{1}{\sqrt{1+P^{2}}}\text{d}P=\int_{}^{}a\text{d}x=ax+c_{2}\] Now let’s calculate \(\int_{}^{} \frac{1}{\sqrt{1+P^{2}}}\text{d}P\), \[J=\int_{}^{} \frac{1}{\sqrt{1+P^{2}}}\text{d}P\] Let \(P=\tan\alpha\Rightarrow\text{d}P=\left(\sec\alpha\right)^{2}\text{d}\alpha\) \[J=\int_{}^{} \frac{1}{\sqrt{1+\left(\tan\alpha\right)^{2}}}\left(\sec\alpha\right)^{2}\text{d}\alpha\] We have \(1+\left(\tan\alpha\right)^{2}=\left(\sec\alpha\right)^{2}\) \[J=\log\mid\sec\alpha+\tan\alpha\mid\] We have \(\tan\alpha=P\) and \(\sec\alpha=\sqrt{1+\left(\tan\alpha\right)^{2}}=\sqrt{1+P^{2}}\) \[\Rightarrow J=\log\mid P+\sqrt{1+P^{2}}\mid+c_{1}\] \(P=\frac{\text{d}y}{\text{d}x}\geq0\) because the curve is increasing when \(x\geq0\) (the graph is symmetric about \(y-axis\) it is enough to deal with \(x\geq0\)) and we have \(\sqrt{1+P^{2}}>0\) therefore, \[J=\log \left(P+\sqrt{1+P^{2}}\right)+c_{1}\] Now, let’s get back to the main problem \[\int_{}^{} \frac{1}{\sqrt{1+P^{2}}}\text{d}P=\int_{}^{}a\text{d}x=ax+c_{2}\] \[\Rightarrow\log \left(P+\sqrt{1+P^{2}}\right)+c_{1}=ax+c_{2}\] \[\Rightarrow\log \left(P+\sqrt{1+P^{2}}\right)=ax+c_{3}\] For \(x=0\Rightarrow\frac{\text{d}y}{\text{d}x}=P=0\Rightarrow\log \left(0+\sqrt{1+0^{2}}\right)=a0+c_{3}\Rightarrow c_{3}=0\) Thus, \[\log \left(P+\sqrt{1+P^{2}}\right)=ax\Rightarrow P+\sqrt{1+P^{2}}=e^{ax}\] Using conjugate, we get \[e^{ax}\sqrt{1+P^{2}}-e^{ax}P=1\] \[\Rightarrow\left(e^{ax}\sqrt{1+P^{2}}\right)^{2}=\left(1+e^{ax}P\right)^{2}\] \[\Rightarrow1+2e^{ax}P=e^{2ax}\] \[\Rightarrow P=\frac{e^{2ax}-1}{2e^{ax}}\] Therefore \[\Rightarrow P=\frac{\text{d}y}{\text{d}x}=\frac{e^{ax}-e^{-ax}}{2}\] \[\Rightarrow \int_{}^{} \text{d}y=\int_{}^{} \frac{e^{ax}-e^{-ax}}{2}\text{d}x\] Finally \[\color{green} {\large y=\frac{\cosh\left(ax\right)}{a}+c}\]
Home -> Solved problems -> Catenary problem
Every problem you tackle makes you smarter.
↓ Scroll down for more maths problems↓
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?