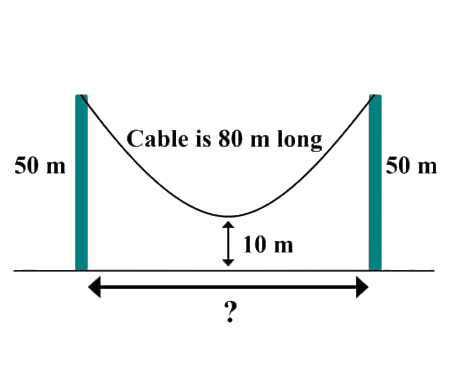
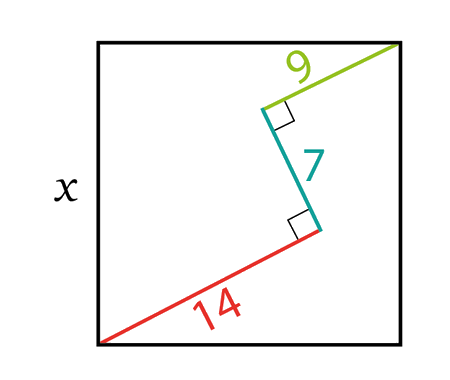
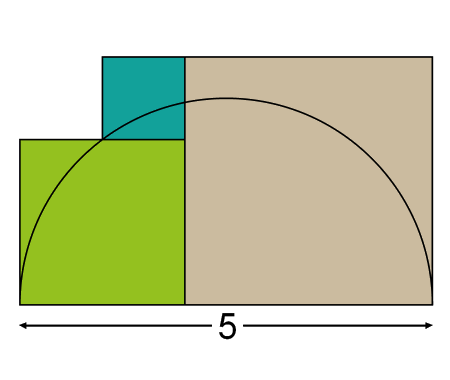
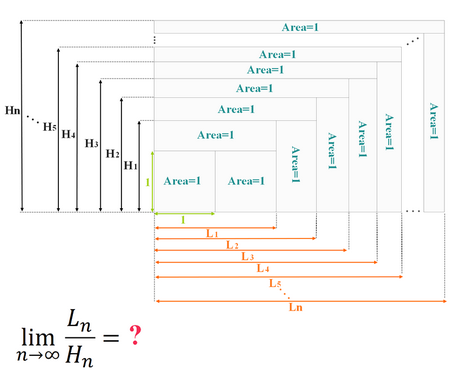
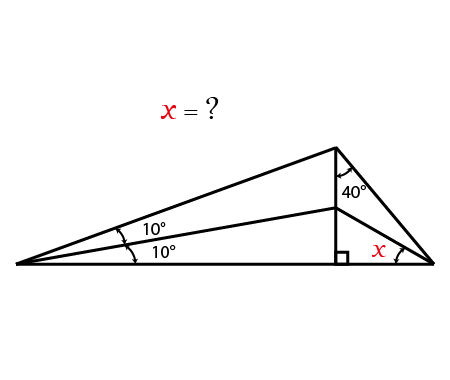
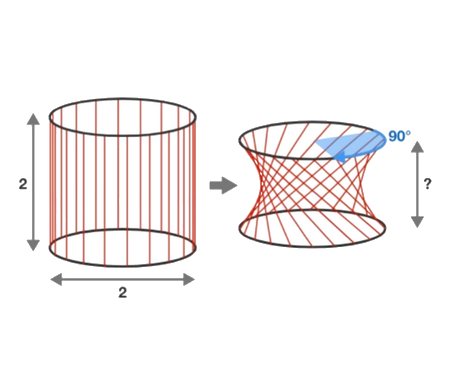
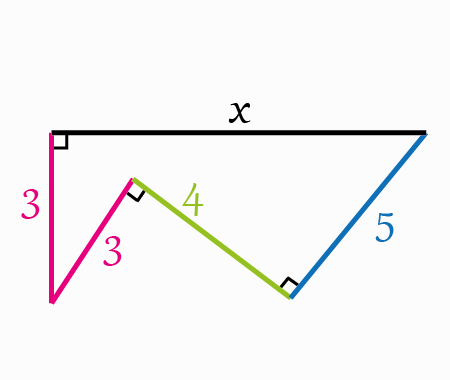
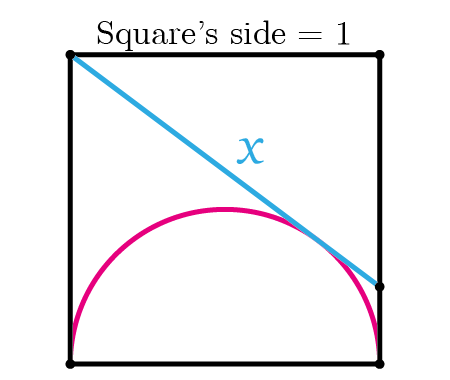
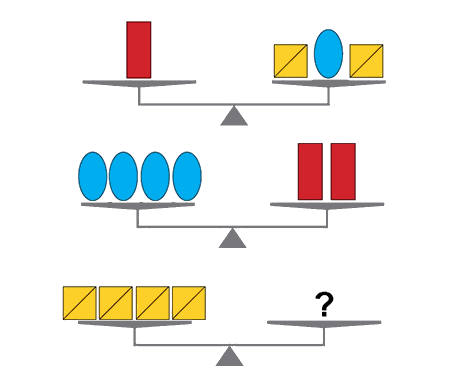
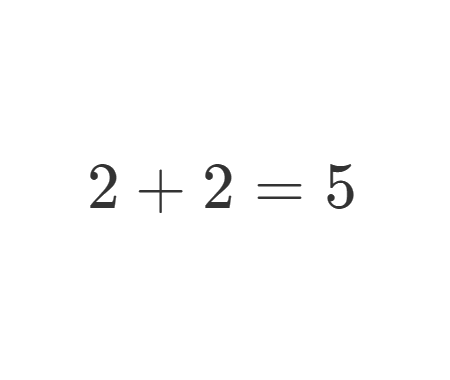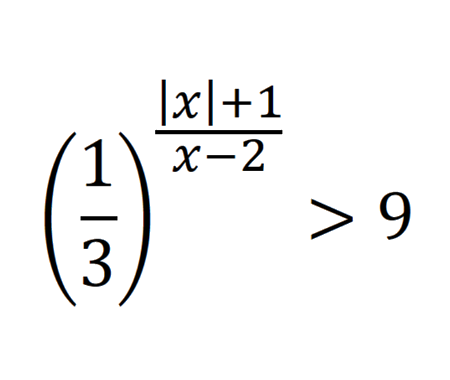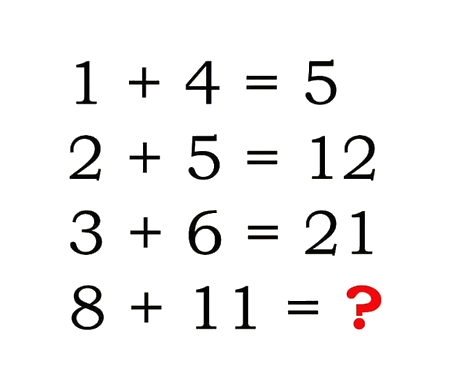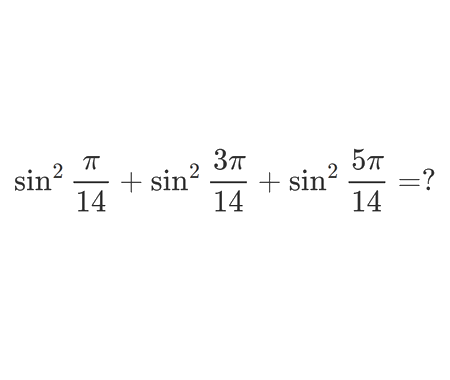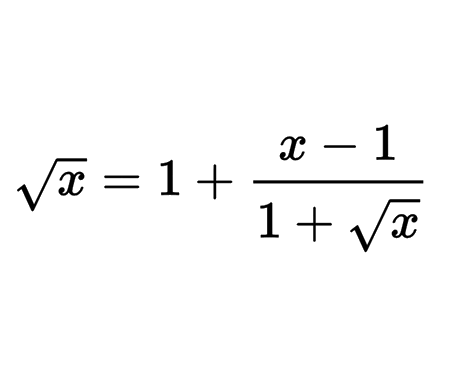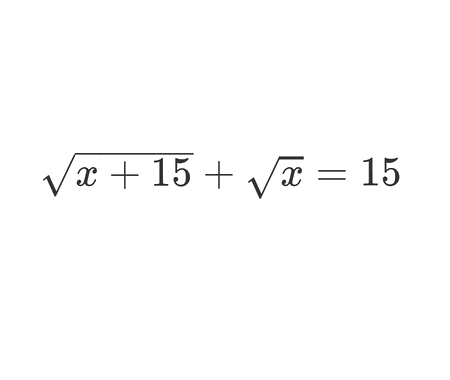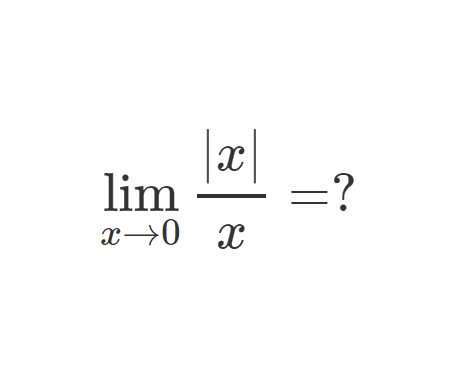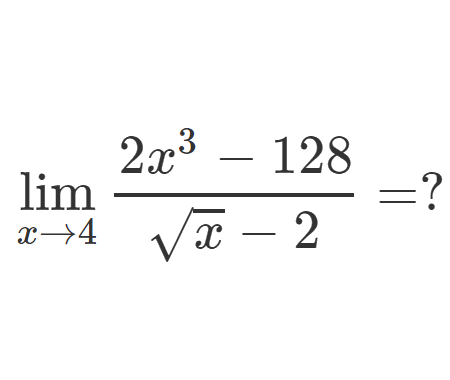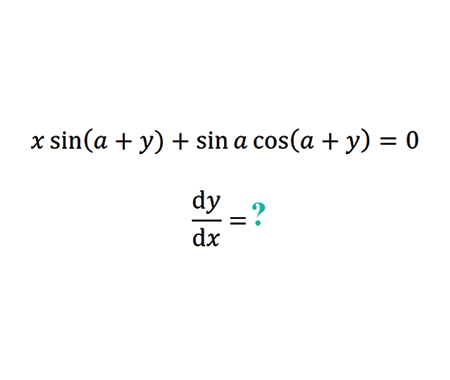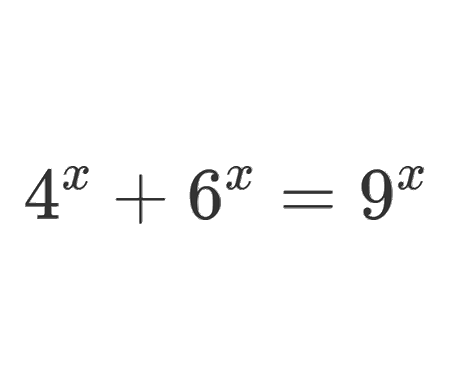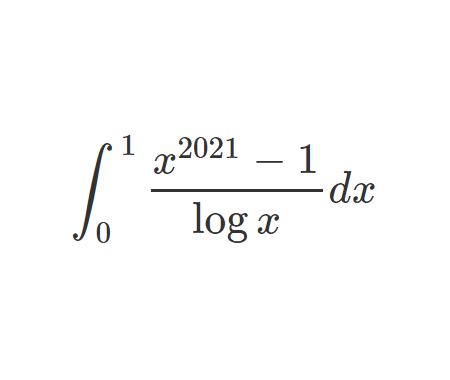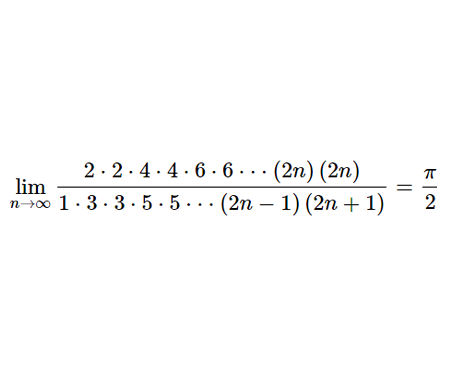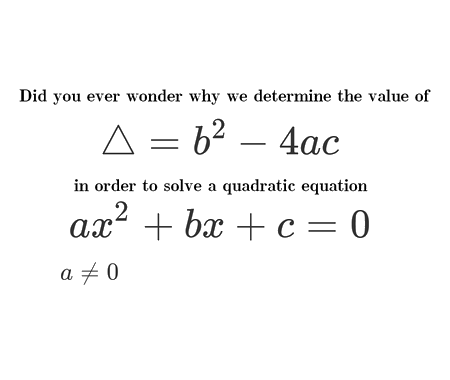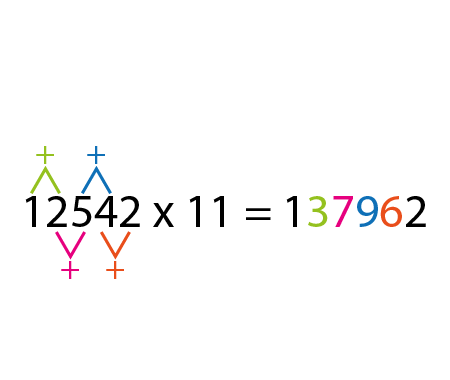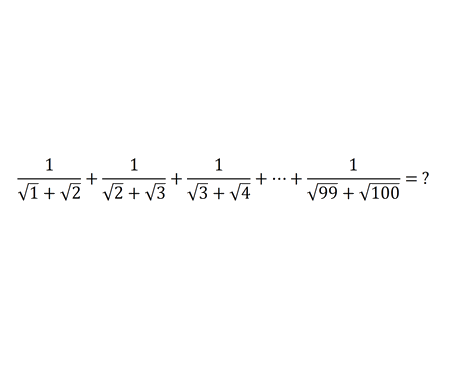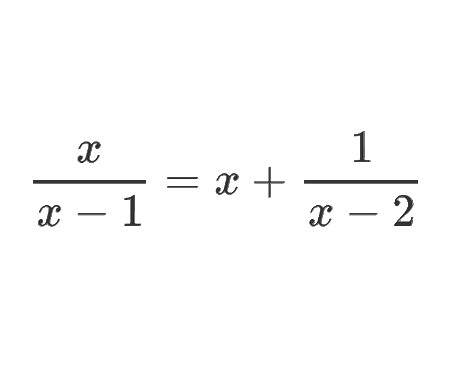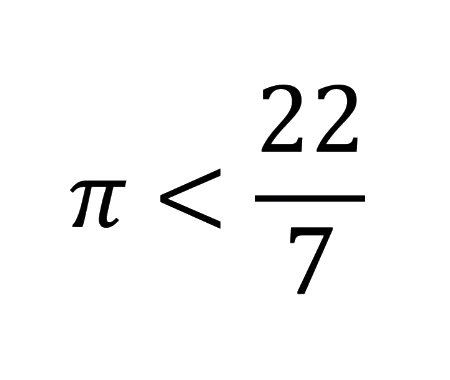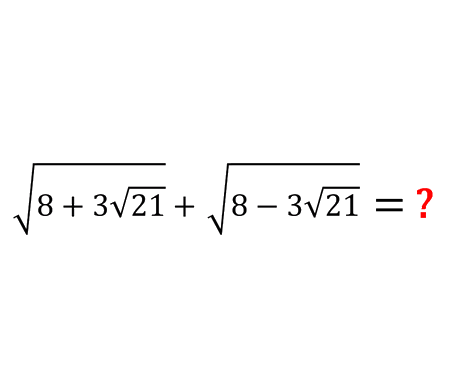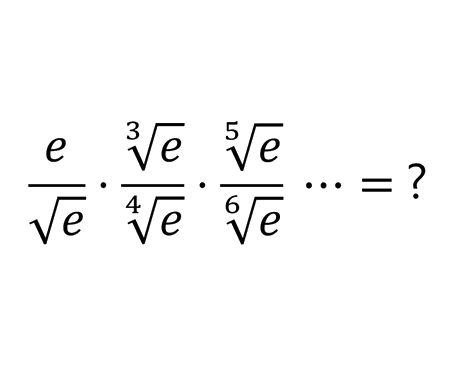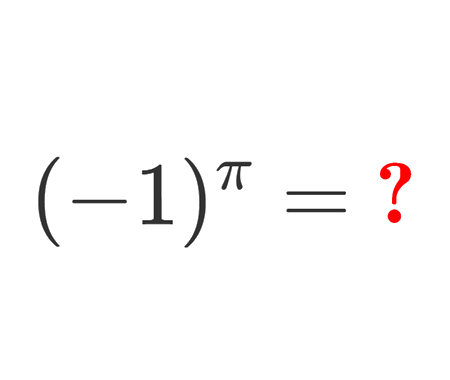Error to avoid that leads to:
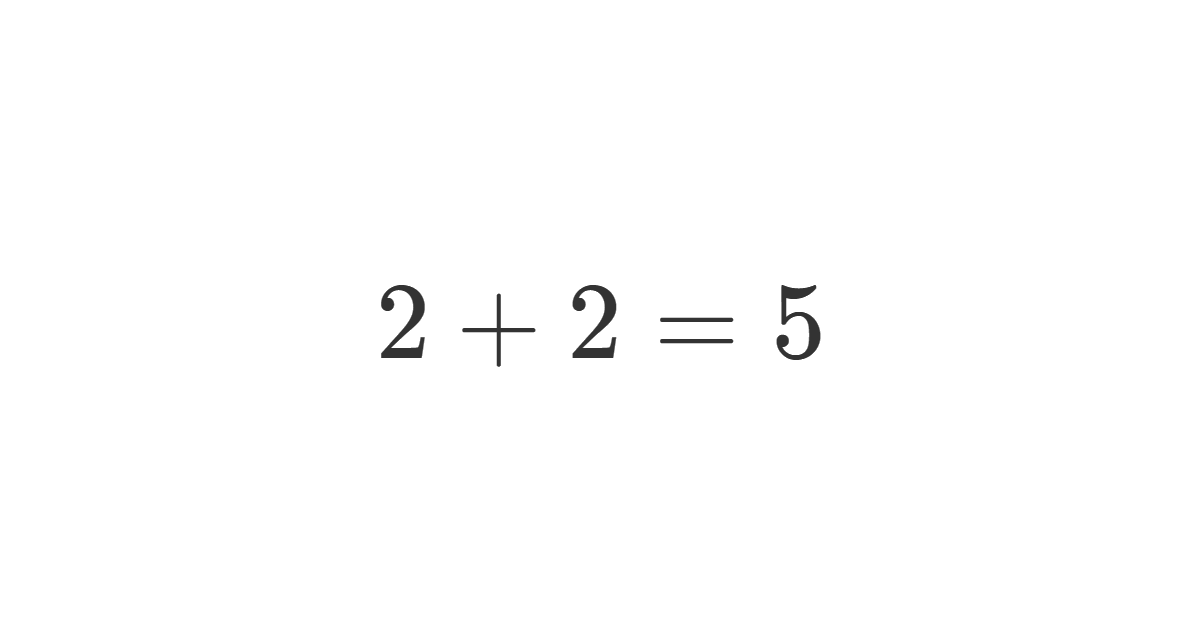
Solution
In this example we examine a subtle but critical algebraic mistake: assuming that
\(\sqrt{x^2} = x\) for all real \(x\).
This flawed assumption can lead to absurd “proofs,” like the false statement 2 + 2 = 5.
Understanding why the correct identity is actually \(\sqrt{x^2} = |x|\) is essential for correct algebraic manipulation.
This proof error 2 + 2 = 5 shows how a subtle step involving the square root and absolute value leads to a false conclusion. It demonstrates the importance of handling \(\sqrt{x^2} = |x|\) correctly in algebra.
The key takeaway is that \(\sqrt{x^2}\) is not always equal to \(x\); it equals the absolute value \(|x|\).
Overlooking this fact can cause serious logical errors, like “proving” 2 + 2 = 5.
By being precise about the definition of square roots and absolute values, you avoid such pitfalls and deepen your understanding of algebraic reasoning.
For more solved exercises and visual proofs, check our Solved Exercises page.