Home -> Solved problems -> e^pi or pi^e
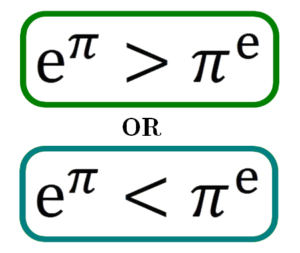
\(\mathrm{e}^{\pi}>\pi^{\mathrm{e}}\;\;\;or\;\;\;\mathrm{e^{\pi } < \pi ^ { \mathrm { e } }}\)

Solution
Let’s solve the problem,
\[\begin{aligned}
&\frac{\pi^{e}}{e^{\pi}}=\frac{\pi^{e}}{e^{\pi-e} e^{e}}\\\\
&=\frac{1}{e^{\pi-e}}\left(\frac{\pi}{e}\right)^{e}\\\\
&=\frac{1}{e^{\pi-e}}\left(1+\frac{\pi}{e}-1\right)^{e}\\\\
&=\frac{1}{e^{\pi-e}}\left(1+\frac{\pi-e}{e}\right)^{e}\\\\
&=\frac{1}{e^{\pi-e}}\left(1+\frac{1}{\frac{e}{\pi-e}}\right)^{\frac{e}{\pi-e} e \frac{\pi-e}{e}}\\\\
&=\frac{1}{e^{\pi-e}}\left(\left(1+\frac{1}{\frac{e}{\pi-e}}\right)^{\frac{e}{\pi-e}}\right)^{\pi-e}
\end{aligned}\]
Let \(f\) the function defined by,
\[f(x)=\left(1+\frac{1}{x}\right)^{x}\]
We know that \(f\) is an increasing function for \(x>0\) and \[\lim _{x \rightarrow\infty}\left(1+\frac{1}{x}\right)^{x}=e\]
\[\begin{aligned}
&\Rightarrow\left(1+\frac{1}{\frac{e}{\pi-e}}\right)^{\frac{e}{\pi-e}} <e\\\\
&\left.\Rightarrow \frac{1}{e^{\pi-e}}\left(\left(1+\frac{1}{\frac{e}{\pi-e}}\right)^{\frac{e}{\pi-e}}\right)^{\pi-e}<\frac{1}{e^{\pi-e}} e^{\pi-e}=1\right.\\\\
&\Rightarrow \frac{\pi^{e}}{e^{\pi}}<1
\end{aligned}\]
\[\huge \Rightarrow e^{\pi}>\pi^{e}\]
Home -> Solved problems -> e^pi or pi^e
Related Topics
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
Home -> Solved problems -> e^pi or pi^e
Share the solution: e^pi or pi^e