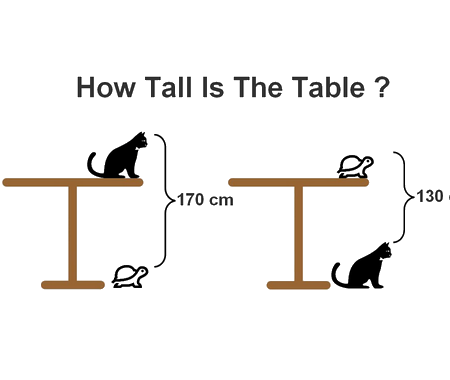
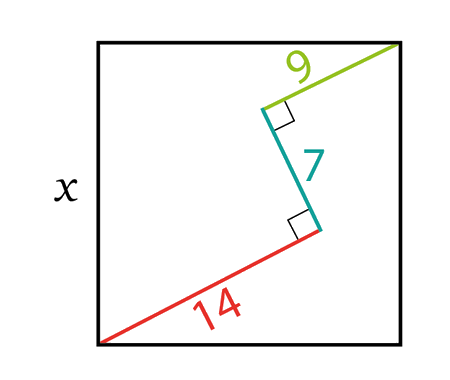
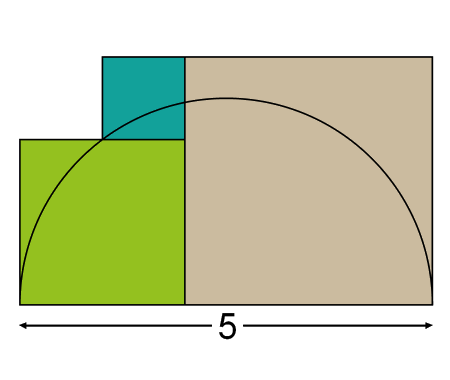
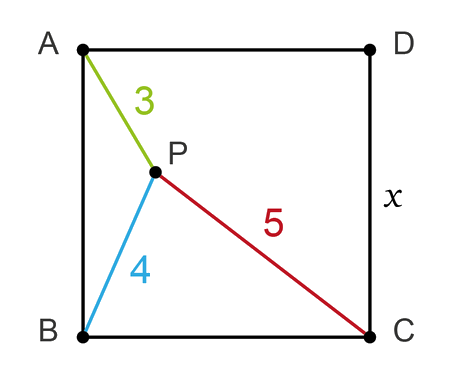
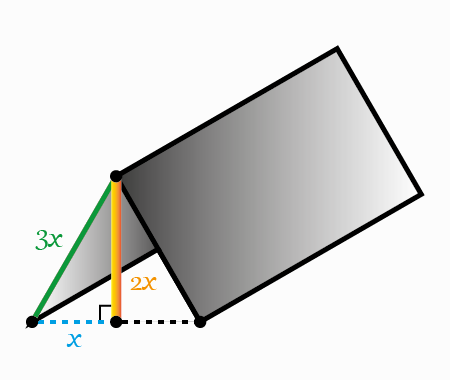
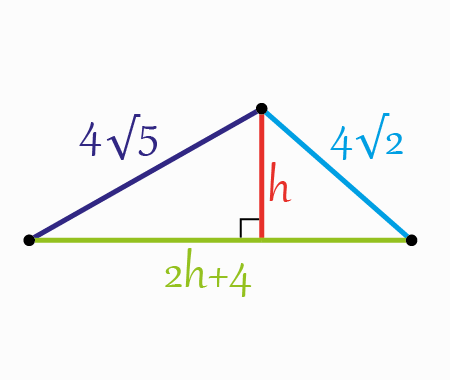
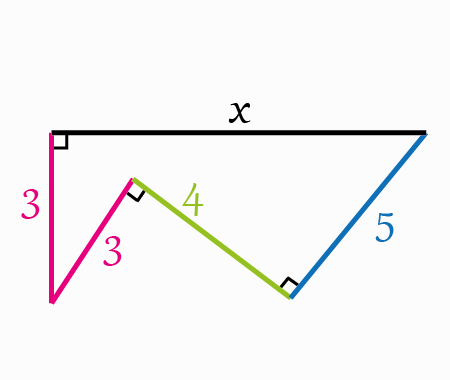
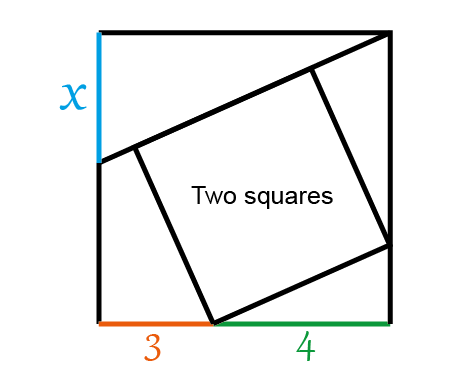
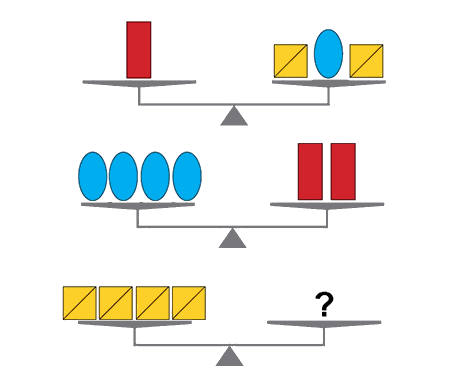
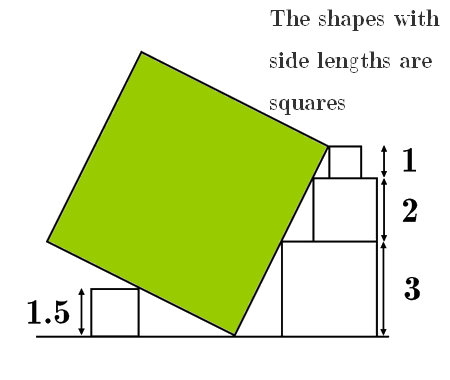
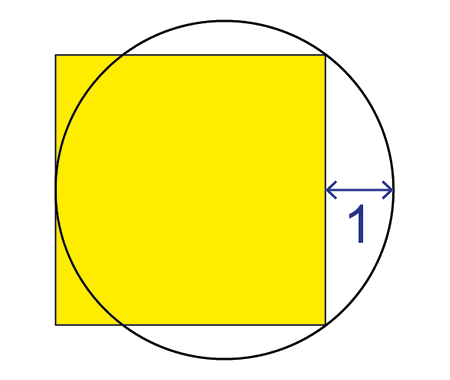
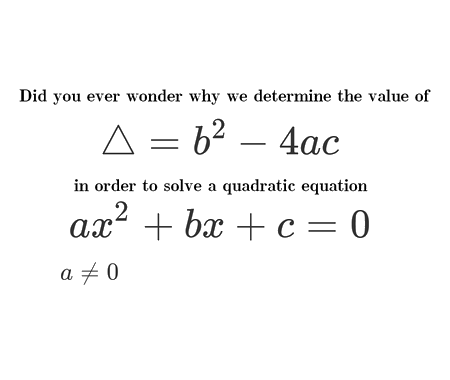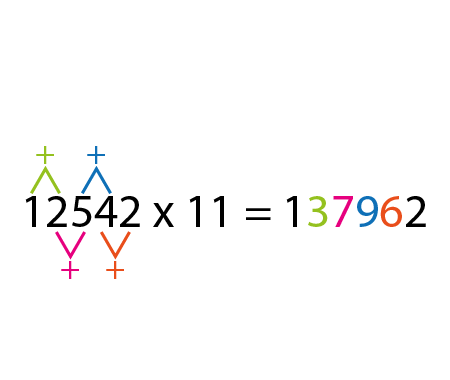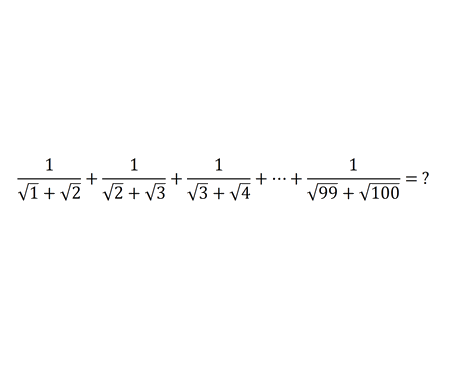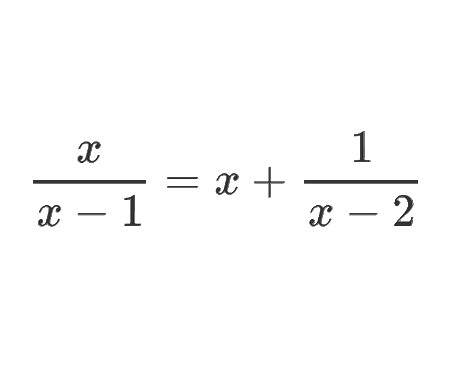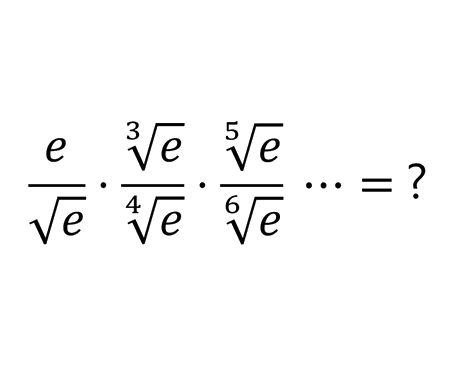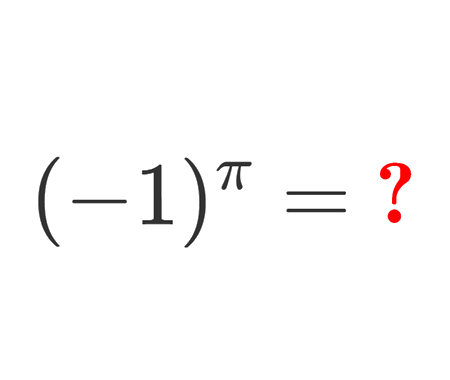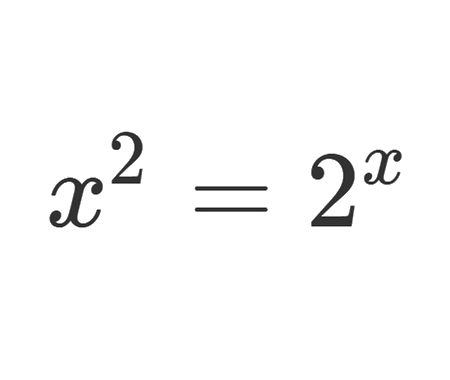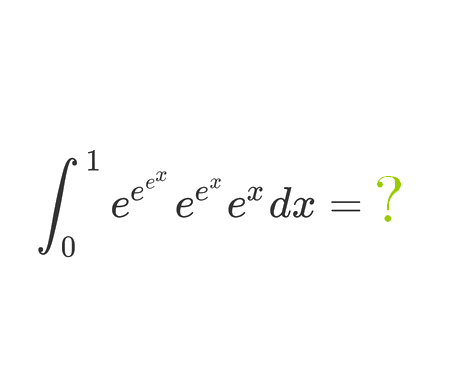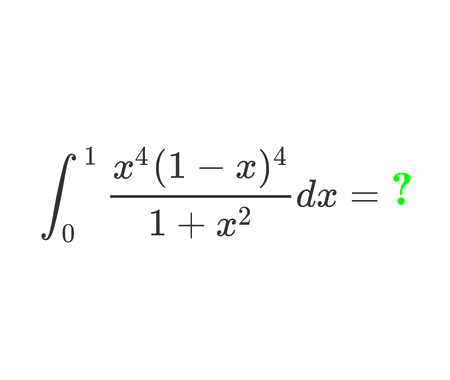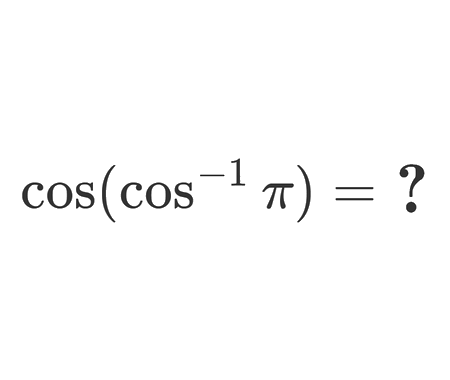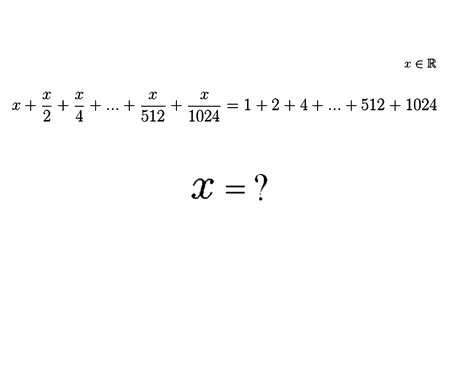Determine the length \(x\) of the blue segment
Home -> Solved problems -> We have two squares, determine the value of x
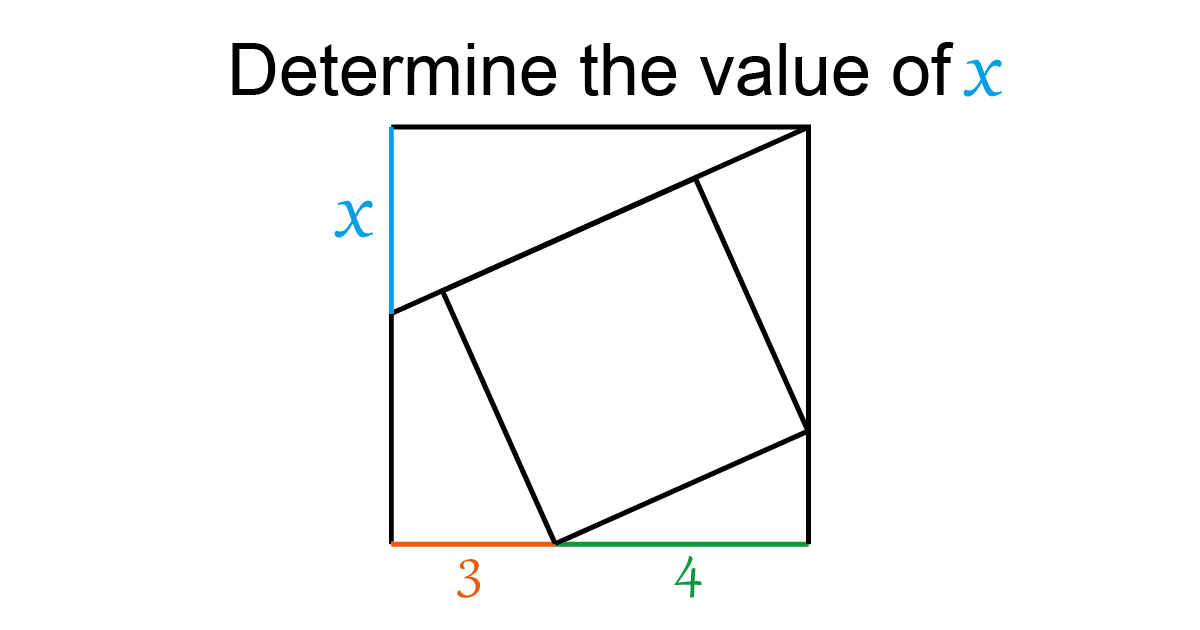
Solution
Let’s add sections like it’s shown in the next figure
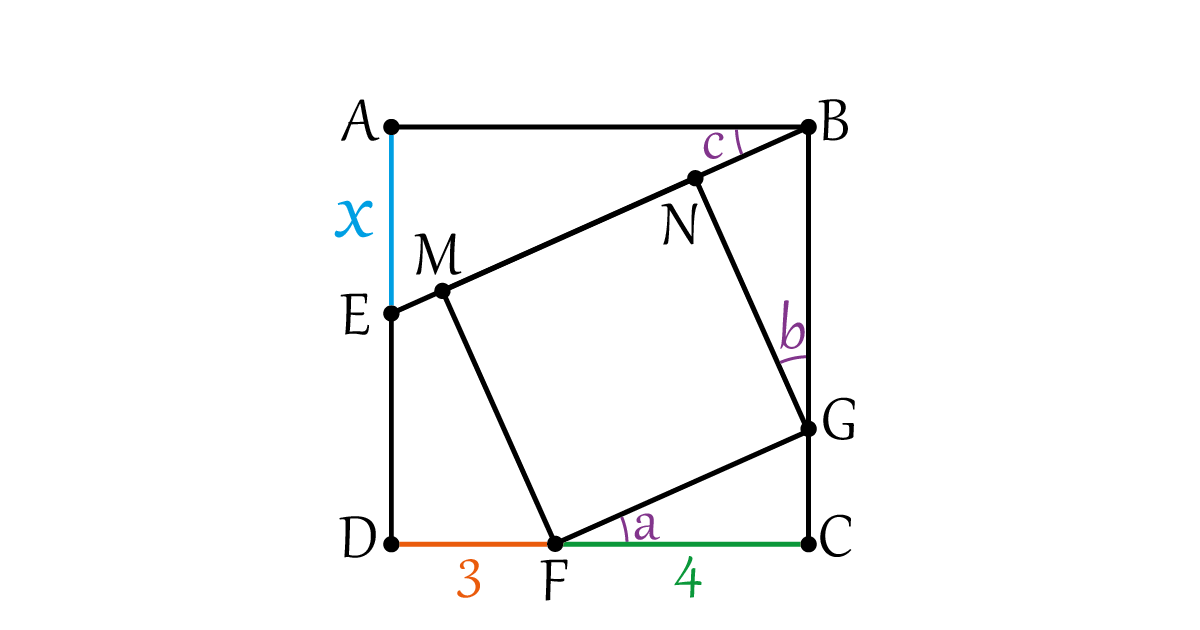
We have two squares \(\square A B C D \) and \(\square M N G F \)
\[\begin{gathered}
A B \| D C\\\\
and\\\\
E B \| F G\\\\
\angle a=\angle c\\\\
Also\\\\ \triangle B A E \\\\and\\\\ \triangle F C G\\\\ are\; Right\; Triangles.\\\\
\triangle B A E \sim \Delta F C G \\\\
\frac{A B}{C F}=\frac{A E}{C G} \\\\
\frac{7}{4}=\frac{x}{C G} \\\\
C G=\frac{4 x}{7}
\end{gathered}
\]
\[\begin{gathered}
\Delta F C G \;is\; a\; Right \;Triangle\\\\
By\;Pythagoras\;theorem\\\\
F G^{2}=C F^{2}+C G^{2}\\\\
F G=\sqrt{4^{2}+\left(\frac{4 x}{7}\right)^{2}}\\\\
F G=\sqrt{16+\frac{16 x^{2}}{49}}=N G
\end{gathered}
\]
\[\begin{aligned}
&\text { From } \Delta G F C \\\\
&\qquad \begin{array}{c}
\angle a+\angle F C G+\angle C G F=180^{\circ} \\\\
\text { also } \\\\
\qquad \angle b+\angle N G F+\angle C G F=180^{\circ} \\\\
\angle a=\angle b \\\\
\Delta F C G \sim \Delta G N B \\\\
\frac{C F}{N G}=\frac{G F}{B G} \\\\
\frac{4}{N G}=\frac{G F}{B G} \\\\
B G=\frac{1}{4}\left(16+\frac{16 x^{2}}{49}\right)
\end{array}
\end{aligned}
\]
\[\begin{gathered}
B C=B G+G C=7 \\\\
4+\frac{4 x^{2}}{49}+\frac{4 x}{7}=7 \\\\
\frac{4 x^{2}}{49}+\frac{4 x}{7}-3=0 \\\\
4 x^{2}+28 x-147=0 \\\\
x=\frac{-28 \pm \sqrt{28^{2}-4 (4) (-147)}}{2 (4)} \\\\
x=\frac{7}{2}\; \text { or }\; x=-\frac{21}{2} \\\\
\huge x=\frac{7}{2}
\end{gathered}\]
Home -> Solved problems -> We have two squares, determine the value of x
Every problem you tackle makes you smarter.
↓ Scroll down for more maths problems↓
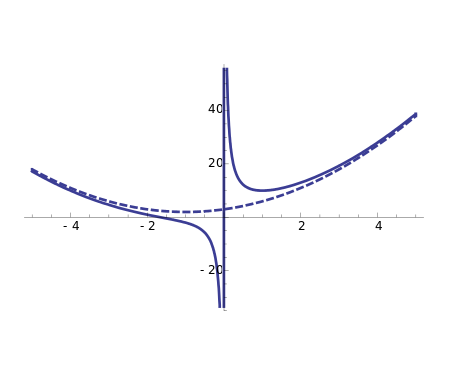
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
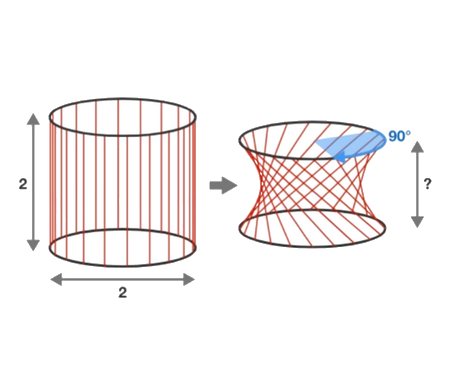
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?
