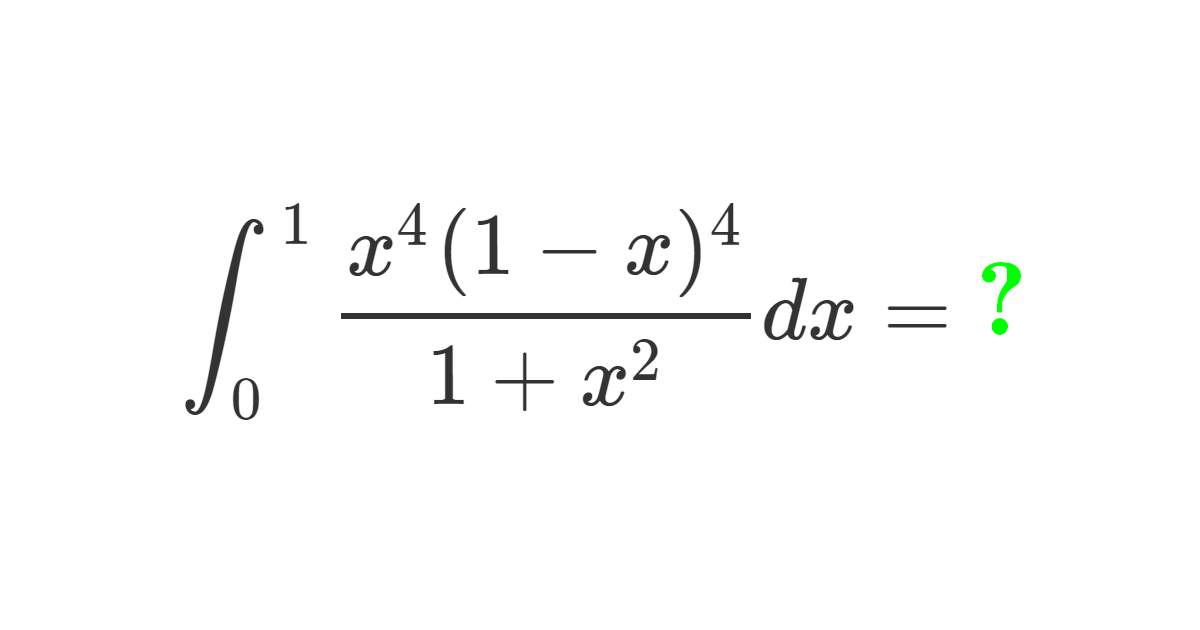
Solution: Evaluate the integral ∫₀¹ (x⁴(1−x)⁴)/(1+x²) dx

Home -> Solved problems -> Calculate the integral

Solution

In this exercise, we aim to evaluate the integral:

$$
I = \int_0^1 \frac{x^4 (1 – x)^4}{1 + x^2} \, dx
$$

This integral beautifully combines algebraic expansion, polynomial division, and calculus techniques.
By applying the binomial theorem to expand $(1 – x)^4$ and simplifying the resulting rational expression,
we can integrate each term step by step to reach an elegant result involving $ \pi $.

Such problems are not only common in calculus but also serve as an excellent example of how symbolic manipulation
and trigonometric functions can reveal deep mathematical relationships.

\[\int_{0}^{1} \frac{x^{4}(1-x)^{4}}{1+x^{2}} d x=?\]

The integral is well defined. Next, let’s use the binomial theorem

\[(1-x)^{4}=x^{4}-4 x^{3}+6 x^{2}-4 x+1\]

\[x^{4}(1-x)^{4}=x^{8}-4 x^{7}+6 x^{6}-4 x^{5}+x^{4}\]

Now, let’s use polynomial division, we get

\[\frac{x^{4}(1-x)^{4}}{1+x^{2}}=x^{6}-4 x^{5}+5 x^{4}-4 x^{2}+4-\frac{4}{x^{2}+1}\]

\[\Rightarrow \int_{0}^{1} \frac{x^{4}(1-x)^{4}}{1+x^{2}} d x=\int_{0}^{1}\left(x^{6}-4 x^{5}+5 x^{4}-4 x^{2}+4-\frac{4}{x^{2}+1}\right) d x\]

\[=\frac{x^{7}}{7}-\frac{4 x^{6}}{6}+x^{5}-\frac{4 x^{3}}{3}+4 x-\left.4 \arctan (x)\right|_{0} ^{1}\]

\[=\frac{1}{7}-\frac{4}{6}+1-\frac{4}{3}+4-4\left(\frac{\pi}{4}\right)-(0-0+0-0+0-4(0))\]

\[=\frac{22}{7}-\pi\]

This result is fascinating because $ \frac{22}{7} $ is a famous historical approximation of $ \pi $,
yet here it appears naturally as part of the exact result of a definite integral.

This demonstrates the deep interconnection between polynomial algebra and transcendental constants,
and highlights the beauty of exact calculus in uncovering mathematical elegance hidden behind seemingly complex expressions.

Share the solution on facebook from here :

Home -> Solved problems -> Calculate the integral

Every problem you tackle makes you smarter.

↓ Scroll down for more maths problems↓

How Tall Is The Table ?

How far apart are the poles ?

Determine the square's side $x$

Find the volume of the interior of the kiln

Solve the equation for real values of $x$

Find the equation of the curve formed by a cable suspended between two points at the same height

Why 0.9999999...=1

Calculate the integral

Error to avoid that leads to:

What's the problem ?

Explain your answer without using calculator

Calculate the sum of areas of the three squares

What values of $x$ satisfy this inequality

Prove that the function $f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x} $ has a curvilinear asymptote $y=x^{2}+2 x+3$

Why does the number $98$ disappear when writing the decimal expansion of $\frac{1}{9801}$ ?

Only one in 1000 can solve this math problem

Calculate the following

Find the limit of width and height ratio

Is $\pi$ an irrational number ?

Solve for $x \in \mathbb{R}$

Prove that $e$ is an irrational number

Prove that

Challenging problem

Solve the equation for $x \in \mathbb{R}$

Calculate the following limit

Determine the angle $x$

Find the derivative of $y$ with respect to $x$

Prove Wallis Product Using Integration

Calculate the radius R

Calculate the volume of Torus using cylindrical shells

Find the derivative of exponential $x$ from first principles

Find the volume of the square pyramid as a function of $a$ and $H$ by slicing method.

Prove that \[\lim_{x \rightarrow 0}\frac{\sin x}{x}=1\]

Prove that

Calculate the half derivative of $x$

Find out what is a discriminant of a quadratic equation.

Calculate the rectangle's area

Infinitely nested radicals

Determine the square's side $x$

Wonderful math fact: 12542 x 11 = 137962

Calculate the sum

What is the new distance between the two circles ?

Solve the equation for $x\epsilon\mathbb{R}$

Calculate the area of the Squid Game diagram blue part

Calculate the limit

Find the infinite sum

Calculate the integral

Prove that

Can we set up this tent ?

Find the value of $h$

Is the walk possible?

Find the length of the black segment

Prove that pi is less than 22/7

Find the value of $x$

Amazing !

Prove that

What is the weight of all animals ?

Determine the length $x$ of the blue segment

How many triangles does the figure contain ?

if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?

What is the value of the following infinite product?

Which object weighs the same as the four squares?

What is $(-1)^{\pi}$ equal to?

Can you solve it?

Great Math Problem

Calculate the integral $\int_{0}^{1}(-1)^{x} d x$

Find the general term of the sequence

Find the radius of the blue circles

Determine the area of the green square

Find the area of the square

Calculate the integral

Home -> Solved problems -> Calculate the integral