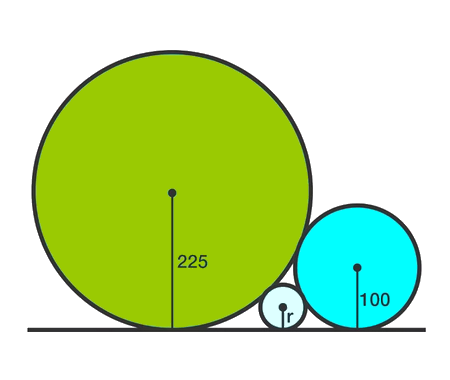
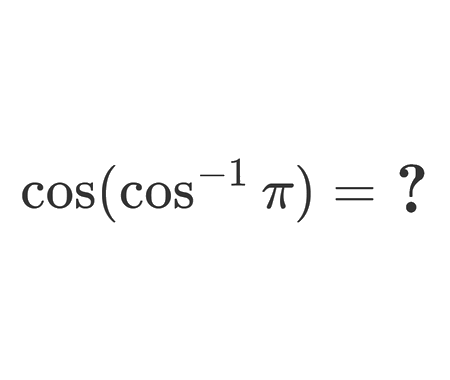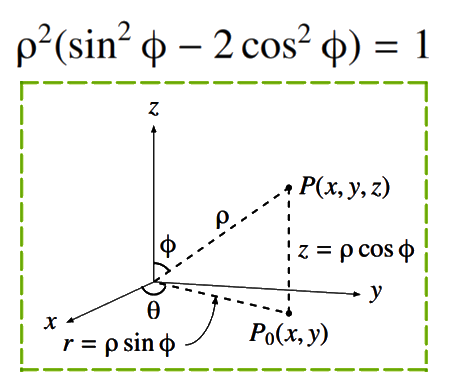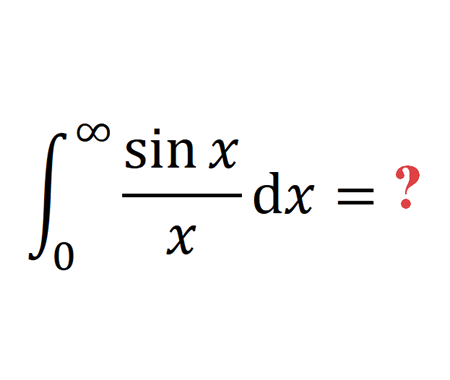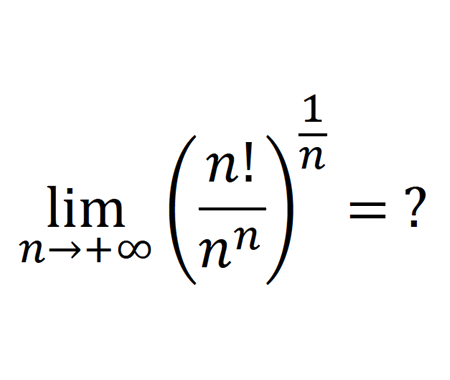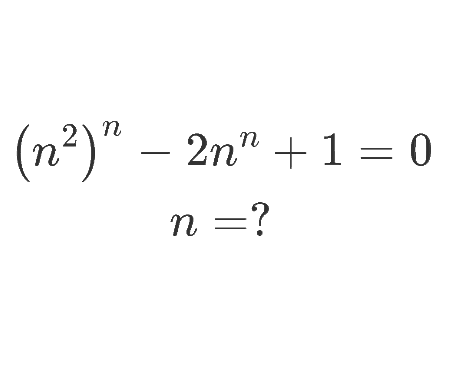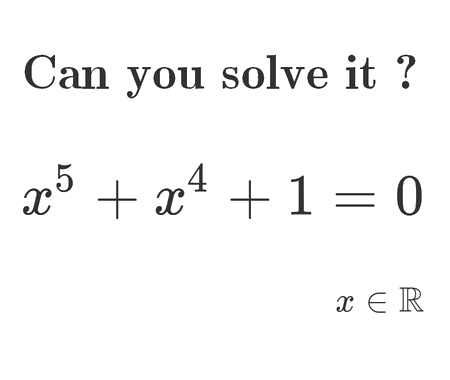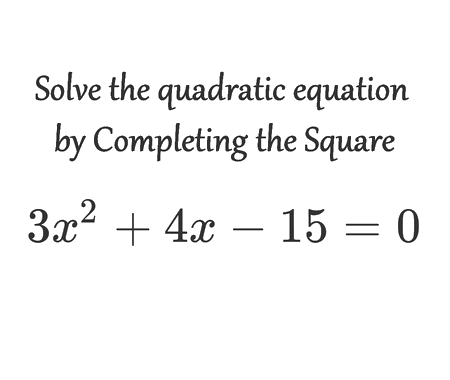Solve the quadratic equation by Completing the Square
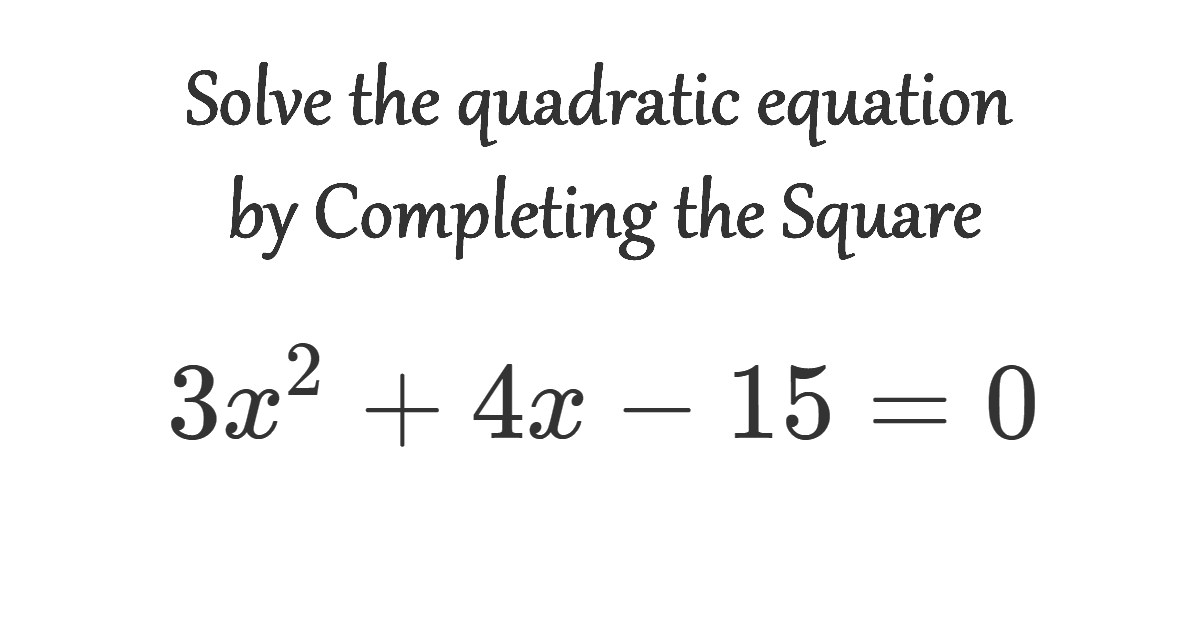
Solution
In this page we demonstrate how to solve a quadratic equation using the completing the square method.
This classical technique rewrites a general form ax² + bx + c = 0 as a perfect square, which simplifies solving for x, even when roots are irrational or complex. :contentReference[oaicite:1]{index=1}
The method also reveals important properties — for example, the vertex of the parabola defined by the quadratic — and forms the basis for the general quadratic formula. :contentReference[oaicite:2]{index=2}
Below, you will see a clear, step-by-step worked example that leads to the full solutions of the equation.
By completing the square, we transformed the quadratic equation into a perfect square trinomial and solved precisely for x.
This method is versatile: it works for any quadratic (even when roots are irrational or complex), and reveals more than just the roots — it also gives insight into the parabola’s vertex and its symmetry.
Remember that the key steps are: normalizing the coefficient of x² to 1 (if needed), moving the constant, adding \((b/2a)^2\) appropriately, then solving the resulting equation.
For more algebraic problems and solutions, feel free to browse our Solved Exercises section.