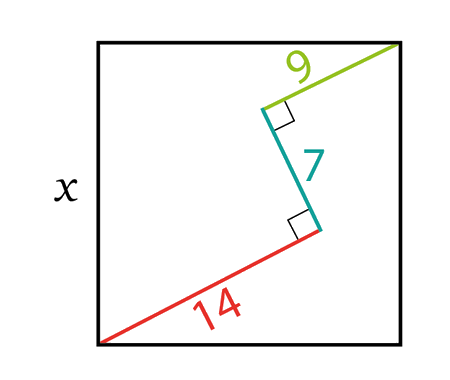
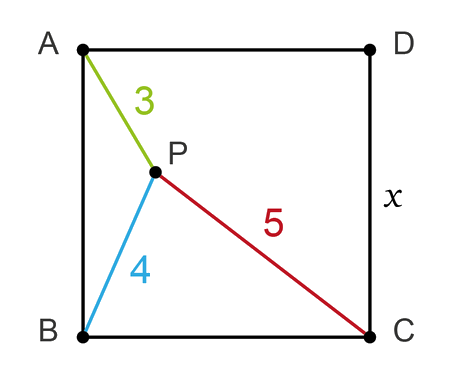
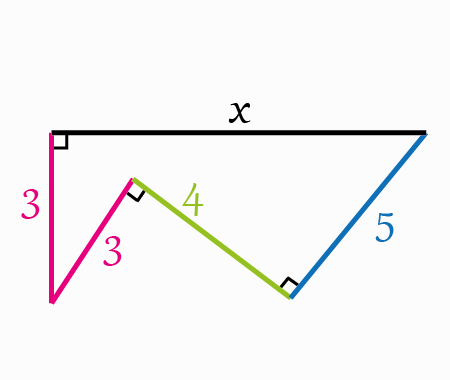
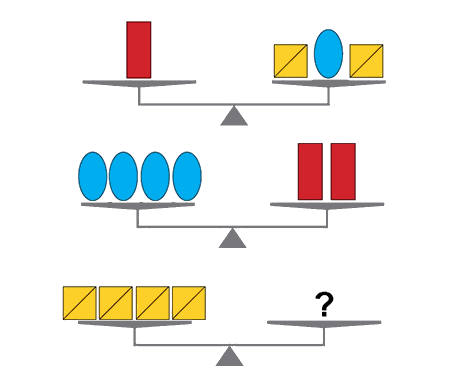
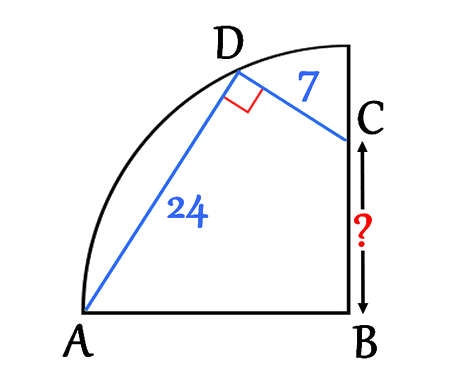
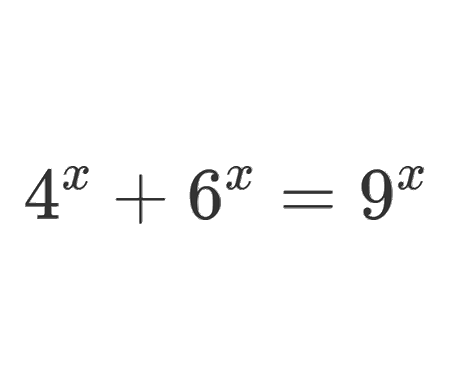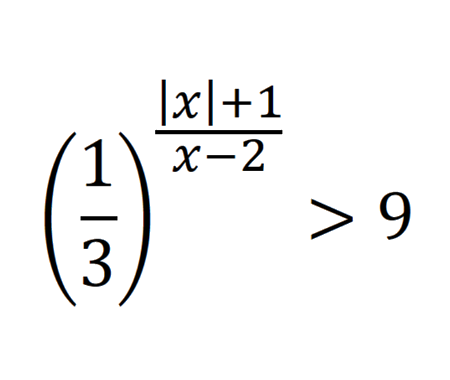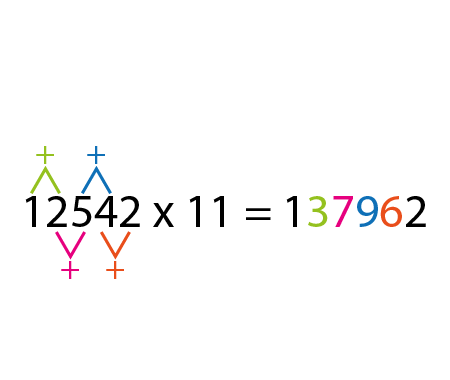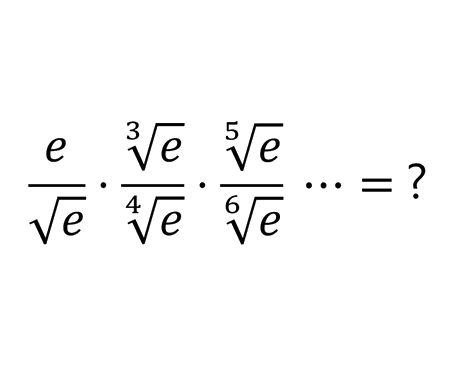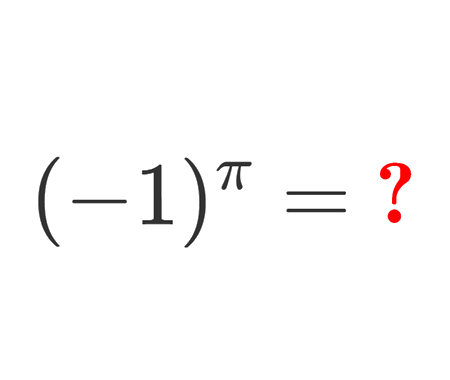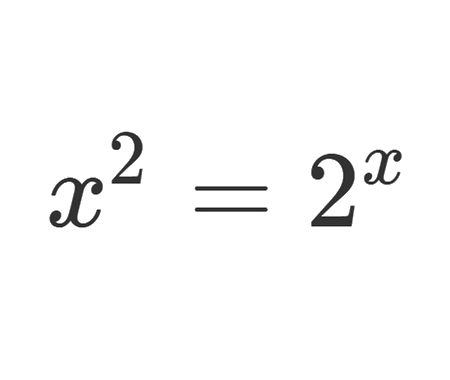Find the distance BC, quarter circle
Home -> Solved problems -> Find the distance BC, quarter circle
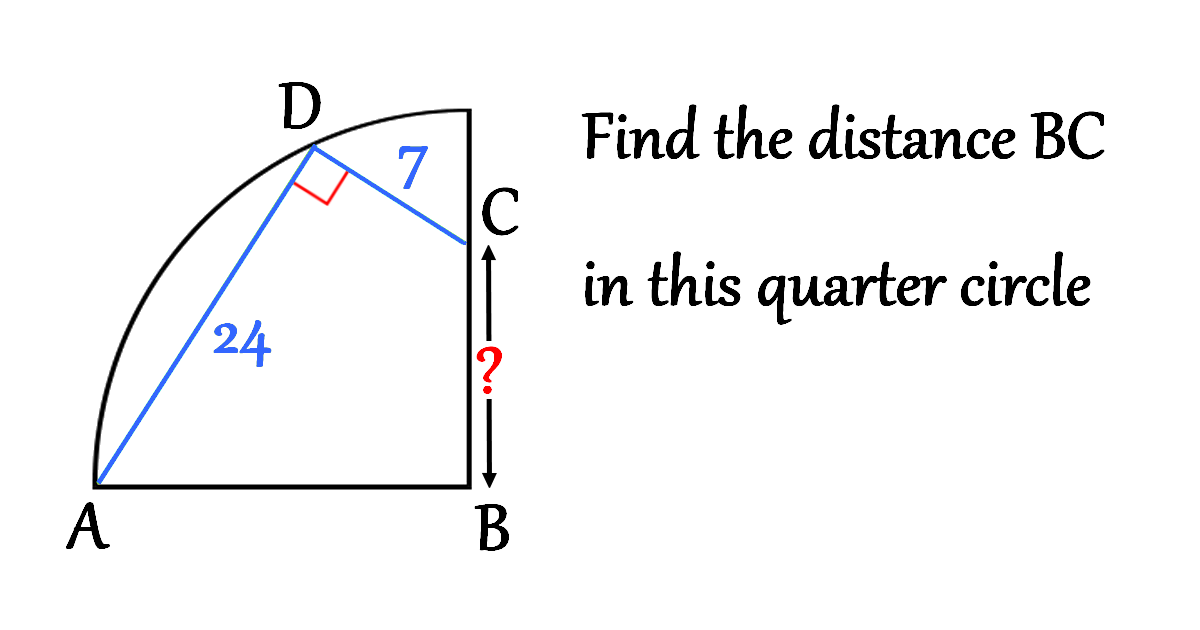
Solution
In this geometric puzzle, we want to determine the distance BC where points A, B, C lie in relation to a quarter circle.
Using right-angle triangles, the Pythagorean theorem, and circle diameter properties, we can derive a clean solution.
The following explanation walks through each reasoning step to show how to arrive at the correct value for BC.
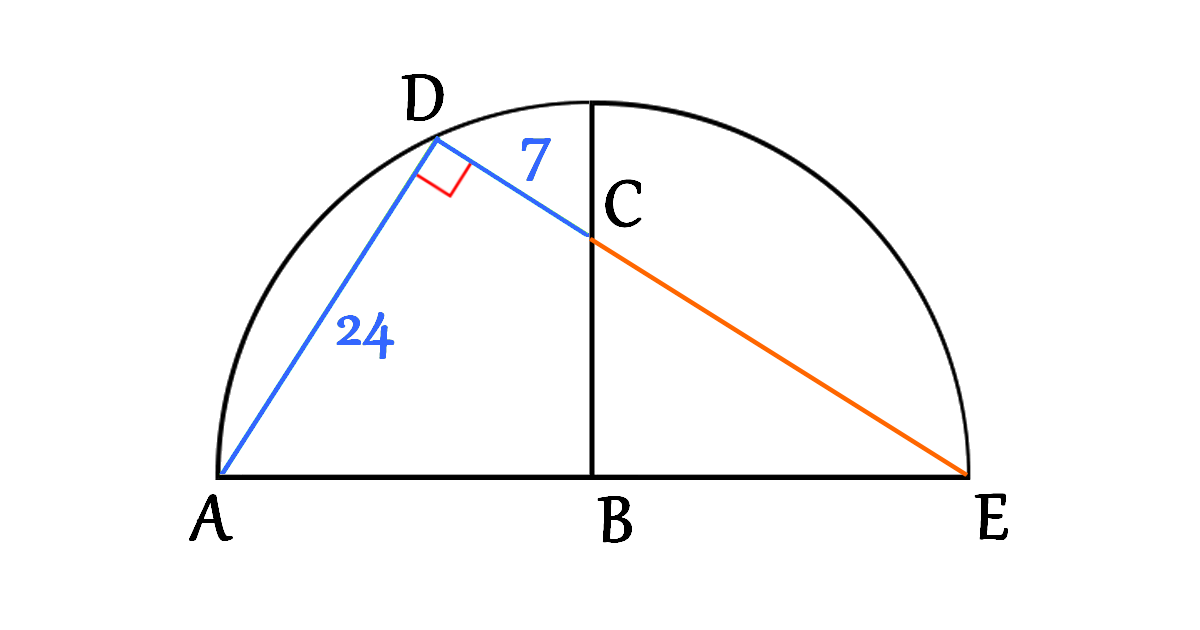
We have a right angle at the point \(D\), thus the line \(CD\) can be extended to a point \(E\) such that \(AE\) is a diameter of the circle like it is shown in the next figure
Now, let’s connect the two points \(A\) and \(C\) and focus on the triangle \(\triangle ADC\)
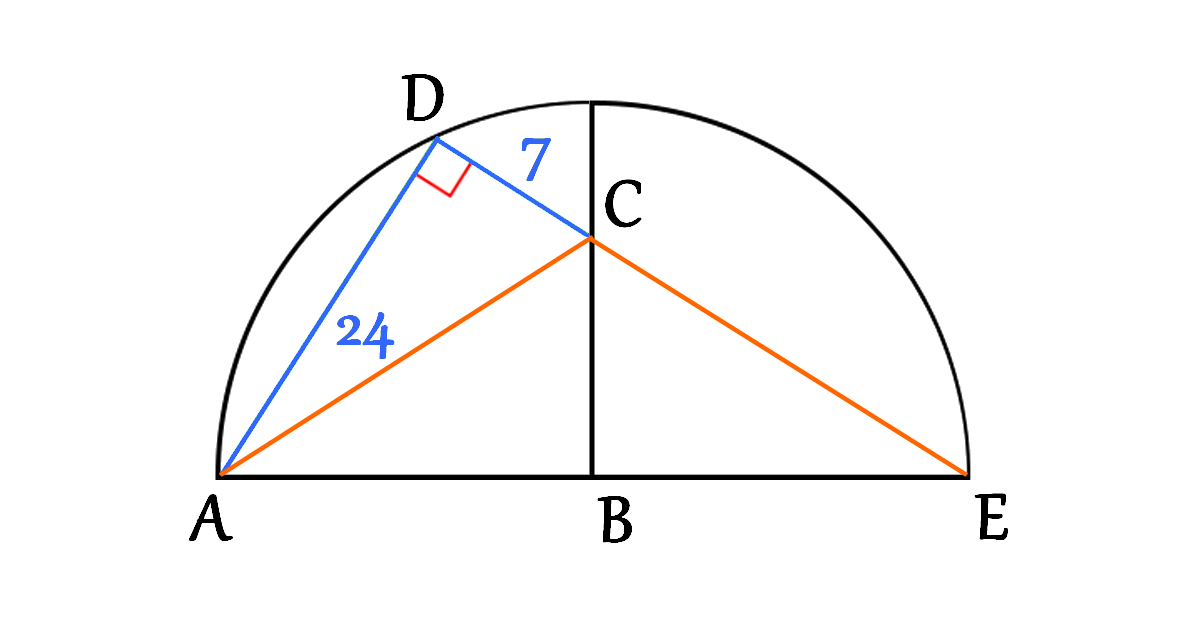
Using Pythagorean theorem
\[\begin{aligned}
A C^{2} &=A D^{2}+D C^{2} \\\\
A C^{2} &=24^{2}+7^{2} \\\\
&=576+49 \\\\
&=625 \\\\
A C &=25
\end{aligned}\]
The triangles \(\triangle ABC\) and \(\triangle EBC\) are congruent triangles, therefore \[CE=AC=25\]
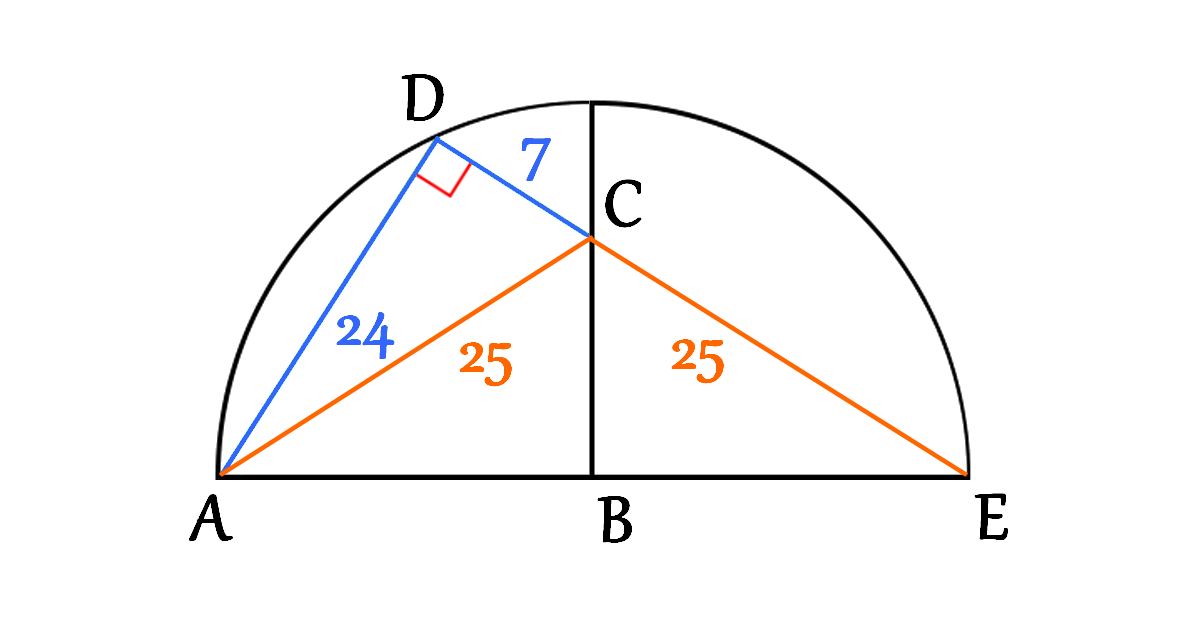
\[\begin{aligned}
&D E=D C+C E \\\\
&D E=7+25 \\\\
&D E=32
\end{aligned}\]
Let’s focus on the triangle \(\triangle ADE\) (Right triangle)
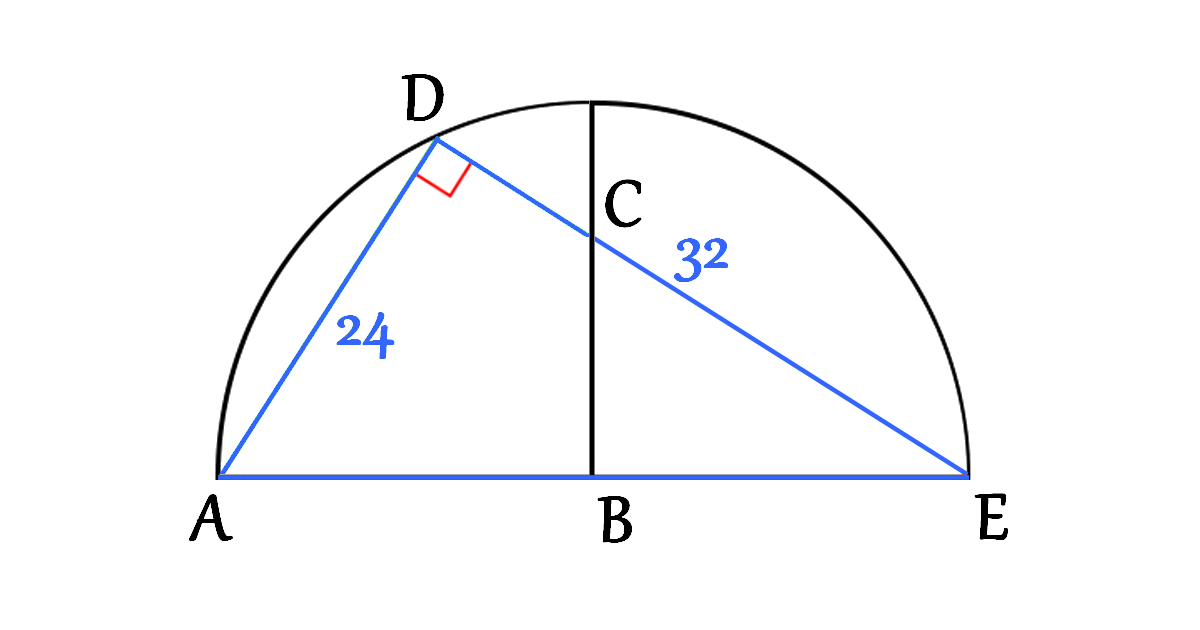
\[\begin{aligned}
A E^{2} &=A D^{2}+D E^{2} \\\\
&=24^{2}+32^{2} \\\\
&=576+1024 \\\\
&=1600 \\\\
A E &=40
\end{aligned}\]
Let’s focus on the triangle \(\triangle BEC\) (Right triangle)
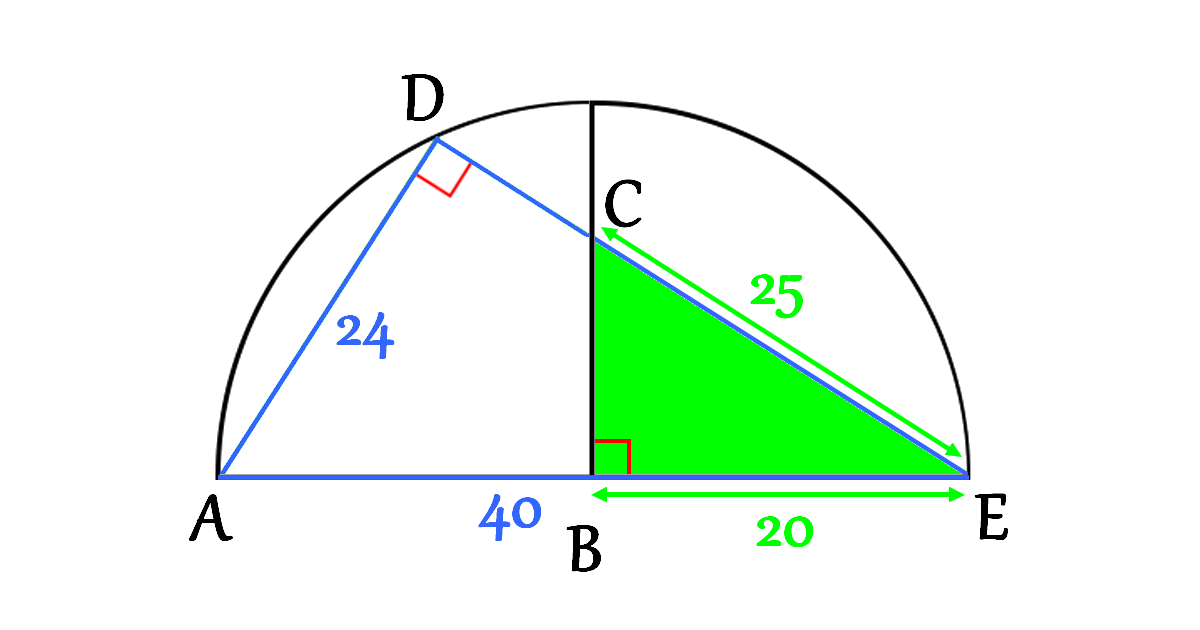
\[\begin{aligned}
C E^{2} &=B C^{2}+B E^{2} \\\\
B C^{2} &=C E^{2}-B E^{2} \\\\
&=25^{2}-20^{2} \\\\
&=625-400 \\\\
&=225 \\\\
B C &=15
\end{aligned}\]
By combining geometry theorems — such as extending chords to form diameters, using the Pythagorean theorem on right triangles, and analyzing congruent triangles — we found that BC = 15.
This problem highlights how classical circle geometry can reveal surprising relationships and how powerful right-triangle reasoning remains in solving circle puzzles.
Home -> Solved problems -> Find the distance BC, quarter circle
Every problem you tackle makes you smarter.
↓ Scroll down for more maths problems↓
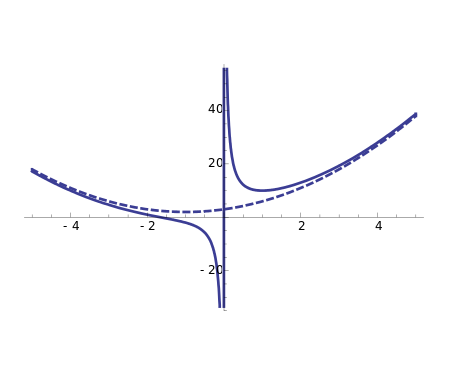
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?