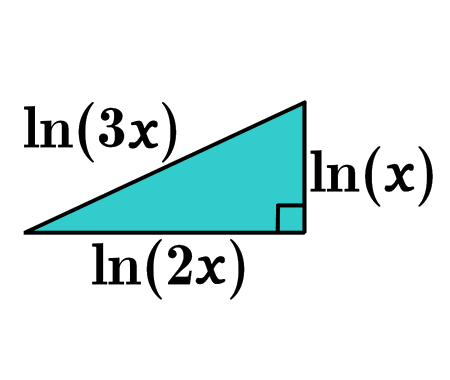How to check if two line segments intersect?
Home -> Solved problems -> How to check if two line segments intersect?
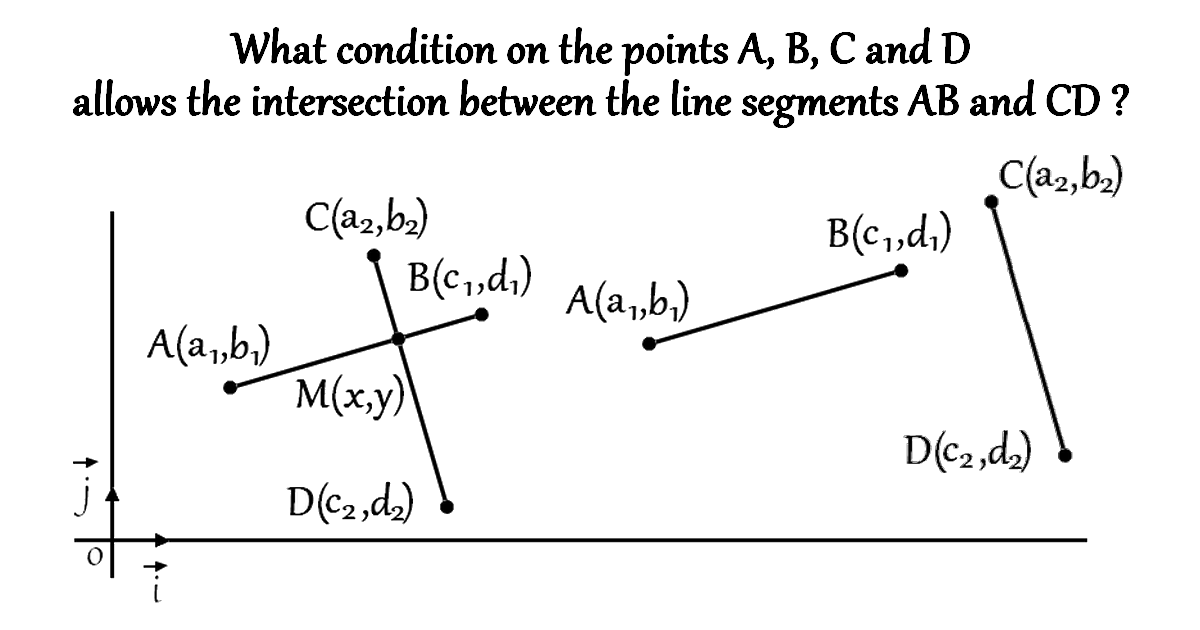
Solution
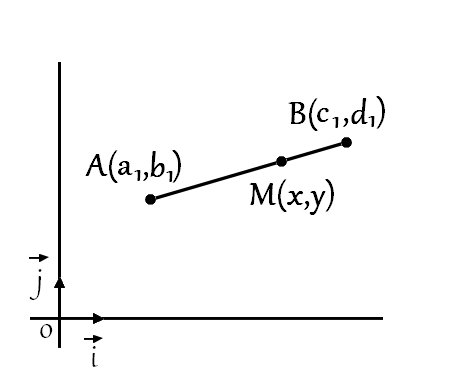
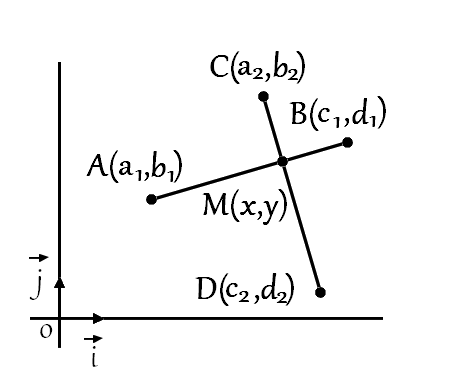
If \(M\) is a point of the line segment \(AB\)
\[\begin{aligned}
\overrightarrow{O M} & =\overrightarrow{O A}+\overrightarrow{A M} \quad, \overrightarrow{A M}=t_1 \overrightarrow{A B}, t_1 \in[0,1] \\\\
& =a_1 \vec{i}+b_1 \vec{j}+t_1\left(\left(c_1-a_1\right) \vec{i}+\left(d_1-b_1\right) \vec{j}\right) \\\\
& =a_1 \vec{i}+t_1\left(c_1-a_1\right) \vec{i}+b_1 \vec{j}+t_1\left(d_1-b_1\right) \vec{j} \\\\
& =\left(a_1+t_1\left(c_1-a_1\right)\right) \vec{i}+\left(b_1+t_1\left(d_1-b_1\right)\right) \vec{j}
\end{aligned}\]
\[\begin{aligned}
& \overrightarrow{O M}=x \vec{i}+y \vec{j} \\\\
& x=a_1+t_1\left(c_1-a_1\right) \\\\
& y=b_1+t_1\left(d_1-b_1\right)
\end{aligned}\]
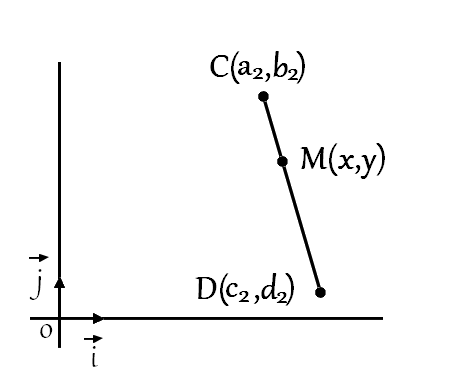
If \(M\) is a point of the line segment \(CD\)
\[\begin{aligned}
& x=a_2+t_2\left(c_2-a_2\right) \\\\
& y=b_2+t_2\left(d_2-b_2\right) \\\\
& t_2 \in[0,1]
\end{aligned}\]
A point \(M(x,y)\) of the plane is common to the line segment \(AB\) and the line segment \(CD\) if and only if, its coordinates \(x\) and \(y\) are solutions of the parametric equations of the two segments:
\[\begin{gathered}
\left\{\begin{array}{c}
x=a_1+t_1 \left(c_1-a_1\right) \\\\
y=b_1+t_1 \left(d_1-b_1\right) \\\\
0\leq t_1\leq1
\end{array}\right. \\\\
\left\{\begin{array}{c}
x=a_2+t_2 \left(c_2-a_2\right) \\\\
y=b_2+t_2 \left(d_2-b_2\right) \\\\
0\leq t_2\leq1
\end{array}\right.
\end{gathered}\]
The line segments \(AB\) and \(CD\) intersect if the following system has at least one solution \((t_1 ,t_2)\), \(0\leq t_1\leq 1\) and \(0\leq t_2\leq 1\):
\[\left\{\begin{array}{l}
a_1+t_1 \left(c_1-a_1\right)=a_2+t_2 \left(c_2-a_2\right) \\
b_1+t_1 \left(d_1-b_1\right)=b_2+t_2 \left(d_2-b_2\right)
\end{array}\right.\]
This system can be rewritten as follows:
\[\left\{\begin{array}{l}
t_1 \left(c_1-a_1\right)-t_2 \left(c_2-a_2\right)=a_2-a_1 \\
t_1 \left(d_1-b_1\right)-t_2 \left(d_2-b_2\right)=b_2-b_1
\end{array}\right.\]
let’s find the determinant
\[\operatorname{det}\left(\left[\begin{array}{ll}
c_1-a_1&-\left(c_2-a_2\right) \\
d_1-b_1&-\left(d_2-b_2\right)
\end{array}\right]\right)=-\left(c_1-a_1\right) \left(d_2-b_2\right)+\left(c_2-a_2\right) \left(d_1-b_1\right)\]
There are several possible cases:
If the determinant is not equal to \(0\) therefore we get a single solution \(t_1\) and \(t_2\). If these are between \(0\) and \(1\) then the two line segments have a single point of intersection.
\[\begin{aligned}
& \text { If } \operatorname{det}\left(\begin{array}{cc}
c_1-a_1 & a_2-c_2 \\
d_1-b_1 & b_2-d_2
\end{array}\right) \neq 0 \\\\
& t_1=\frac{\operatorname{det}\left(\begin{array}{ll}
a_2-a_1 & a_2-c_2 \\
b_2-b_1 & b_2-d_2
\end{array}\right)}{\operatorname{det}\left(\begin{array}{ll}
c_1-a_1 & a_2-c_2 \\
d_1-b_1 & b_2-d_2
\end{array}\right)}\\\\
& t_2=\frac{\operatorname{det}\left(\begin{array}{ll}
c_1-a_1 & a_2-a_1 \\
d_1-b_1 & b_2-b_1
\end{array}\right)}{\operatorname{det}\left(\begin{array}{ll}
c_1-a_1 & a_2-c_2 \\
d_1-b_1 & b_2-d_2
\end{array}\right)}
\end{aligned}\]
\[\begin{aligned}
&\text { If }\\\\
&0 \leqslant t_1 \leqslant 1\\\\&and\\\\ &0 \leqslant t_2 \leqslant 1 \\\\&and\\\\ &c_1 \neq a_1\\\\&and\\\\ &c_2 \neq a_2\\\\&then\\\\
&x=a_1+t_1(c_1−a_1) \\\\
&y=b_1+t_1(d_1−b_1) \\\\
\end{aligned}
\]
– The determinant is not equal to \(0\) but the solutions \(t_1\) and \(t_2\) are not between \(0\) and \(1\) so the two segments do not cross.
In fact, in this case, the lines that extend the line segments have a point of intersection but does not belong to the two line segments.
– The determinant is equal to \(0\). In this case there are either \(0\) solutions (parallel line segments or belong to the same line but have no intersection), or there are infinities of solutions: the two segments “overlap” (their intersection is a line segment).
This is a complete Matlab algorithm for the problem of two line segments intersection. ENJOY!
\[a1=100*rand(1,1);
b1=100*rand(1,1);
c1=100*rand(1,1);
d1=100*rand(1,1);
a2=100*rand(1,1);
b2=100*rand(1,1);
c2=10*rand(1,1);
d2=10*rand(1,1);
A=[c1-a1 d1-b1; a2-c2 b2-d2];
if det(A)~=0
t_1=det([a2-a1 b2-b1;a2-c2 b2-d2])/det([c1-a1 d1-b1;a2-c2 b2-d2]);
t_2=det([c1-a1 d1-b1;a2-a1 b2-b1])/det([c1-a1 d1-b1;a2-c2 b2-d2]);
if (t_1>=0 && t_1<=1) && (t_2>=0 && t_2<=1)
if (c1==a1 && c2~=a2)
cond='YES intersection';
x=a1;
elseif (c1~=a1 && c2==a2)
cond='YES intersection';
x=a2;
elseif (c1~=a1 && c2~=a2)
cond='YES intersection';
x=a1+t_1*(c1-a1);
y=b1+t_1*(d1-b1);
else
cond='NO intersection';
x='NO';
end
else
cond='NO intersection';
x='NO';
end
elseif c1==a1 && c2==a2
if a2==a1
if abs(b1-d1)+abs(b2-d2)==max(max(b1,d1),max(b2,d2))-min(min(b1,d1),min(b2,d2))
cond='YES intersection';
x=a2;
vtri=[b1 d1 b2 d2];
vtri=unique(vtri);
y=vtri(2);
elseif abs(b1-d1)+abs(b2-d2)>max(max(b1,d1),max(b2,d2))-min(min(b1,d1),min(b2,d2))
cond=’intersection is not a point’;
x=’segment’;
else
cond=’NO intersection’;
x=’NO’;
end
else
cond=’NO intersection parallel’;
x=’NO’;
end
elseif d1==b1 && d2==b2
if b2==b1
if abs(a1-c1)+abs(a2-c2)==max(max(a1,c1),max(a2,c2))-min(min(a1,c1),min(a2,c2))
cond=’YES intersection’;
y=b2;
vtri=[a1 c1 a2 c2];
vtri=unique(vtri);
x=vtri(2);
elseif abs(a1-c1)+abs(a2-c2)>max(max(a1,c1),max(a2,c2))-min(min(a1,c1),min(a2,c2))
cond=’intersection is not a point’;
x=’segment’;
else
cond=’NO intersection’;
x=’NO’;
end
else
cond=’NO intersection parallel segments’;
x=’NO’;
end
else
cond=’NO intersection’;
x=’NO’;
end
\]
Home -> Solved problems -> How to check if two line segments intersect?
Every problem you tackle makes you smarter.
↓ Scroll down for more maths problems↓
Find the equation of the curve formed by a cable suspended between two points at the same height
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?
Is it possible to solve for \(x\) so that \(ln(x)\), \(ln(2x)\), and \(ln(3x)\) form a right triangle?