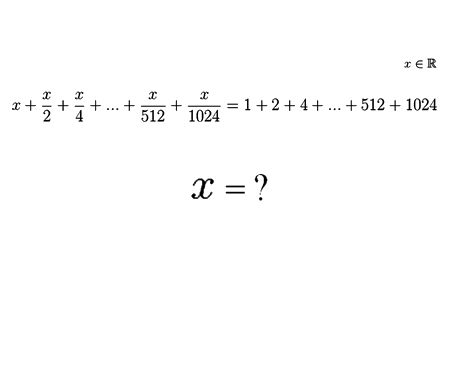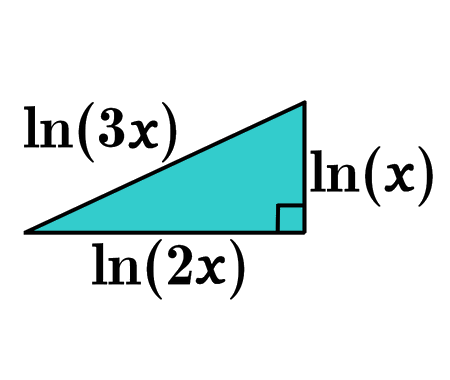Fundamental Theorem of Calculus
Home -> Solved problems -> Fundamental Theorem of Calculus

Solution
The Riemann method includes approximating the area under a curve by rectangular elements.
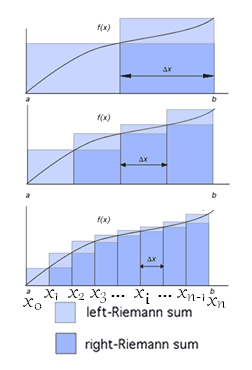
Left-Riemann sum (Area of left-rectangles) :
\[\begin{aligned}
A_1&=f\left(x_0\right) \Delta x+f\left(x_1\right) \Delta x+\ldots+f\left(x_{n-1}\right) \Delta x \\\\
& =\left[f\left(x_0\right)+f\left(x_1\right)+\ldots+f\left(x_{n-1}\right)\right] \Delta x \\\\
& =\sum_{i=0}^{n-1} f\left(x_i\right) \Delta x
\end{aligned}\]
Right-Riemann sum (Area of right-rectangles) :
\[\begin{aligned}
A_r&=f\left(x_1\right) \Delta x+f\left(x_2\right) \Delta x+\ldots+f\left(x_n\right) \Delta x \\\\
& =\left[f\left(x_1\right)+f\left(x_2\right)+\ldots+f\left(x_n\right)\right] \Delta x \\\\
& =\sum_{i=1}^n f\left(x_i\right) \Delta x
\end{aligned}\]
Therefore :
\[\lim_{n \rightarrow \infty}\sum_{i=0}^{n} f\left(x_i\right) \Delta x=\int_a^b f(x) d x\]
Relationship between integration and differentiation :
\(F\) satisfies the hypothesis of the Mean Value Theorem. Let \(P=\left\{x_i\right\}_{i=0}^n\) be a partition of \([a, b]\). Then, we can write
\[
F(b)-F(a)=\sum_{i=1}^n\left[F\left(x_i\right)-F\left(x_{i-1}\right)\right]
\]
Applying the Mean Value Theorem on each subinterval \(\left[x_{i-1}, x_i\right]\) we obtain \(t_i \in\left[x_{i-1}, x_i\right]\) such that \(F^{\prime}\left(t_i\right)=\frac{F\left(x_i\right)-F\left(x_{i-1}\right)}{x_i-x_{i-1}}\) or \(F\left(x_i\right)-F\left(x_{i-1}\right)=F^{\prime}\left(t_i\right)\left(x_i-x_{i-1}\right)\). Since \(F\) is an antiderivative of \(f\), \(F^{\prime}(x)=f(x)\). Also, using the notation of the previous sections, \(x_i-x_{i-1}=\Delta x\) thus we have
\[\begin{aligned}
F(b)-F(a) & =\sum_{i=1}^n\left[F\left(x_i\right)-F\left(x_{i-1}\right)\right] \\\\
& =\sum_{i=1}^n f\left(t_i\right) \Delta x
\end{aligned}\]
This is true for any partition \(P\). Since \(f\) is Riemann integrable, the Riemann sum on the right tends to \(\int_a^b f(x) d x\). Taking the limit on each side as \(\|P\| \rightarrow 0\) completes the proof.
\[\int_a^b f(x) d x=F(b)-F(a)\]
Home -> Solved problems -> Fundamental Theorem of Calculus
Every problem you tackle makes you smarter.
↓ Scroll down for more maths problems↓
Find the equation of the curve formed by a cable suspended between two points at the same height
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?
Is it possible to solve for \(x\) so that \(ln(x)\), \(ln(2x)\), and \(ln(3x)\) form a right triangle?