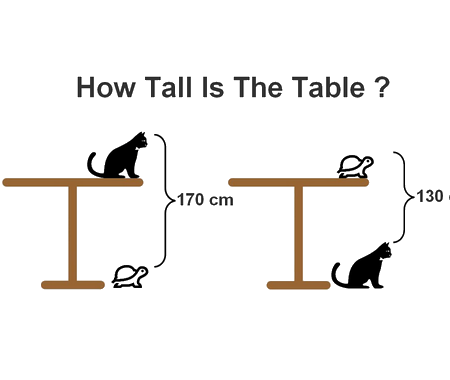
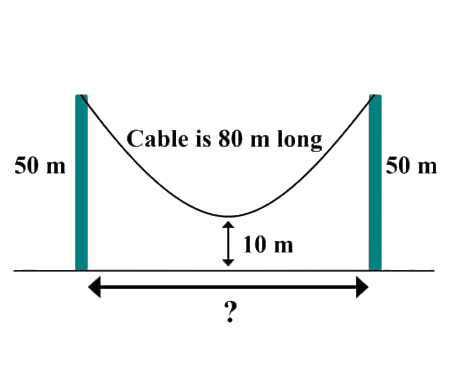
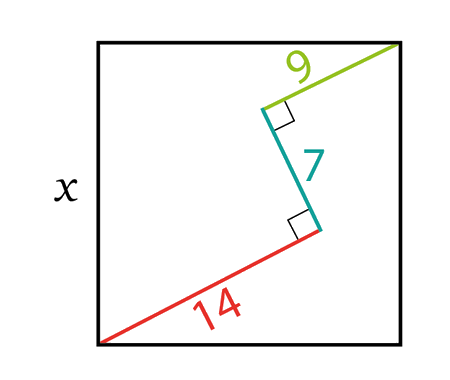
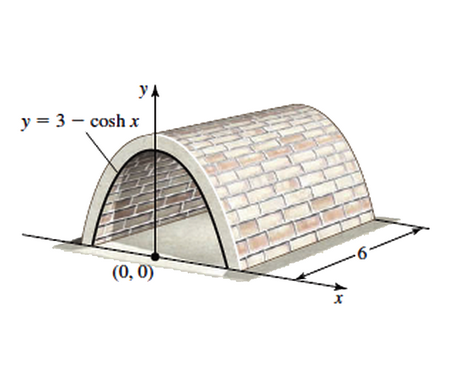
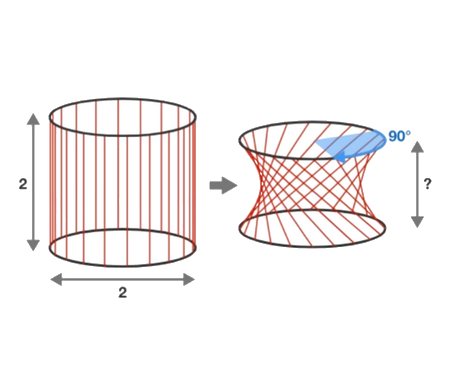
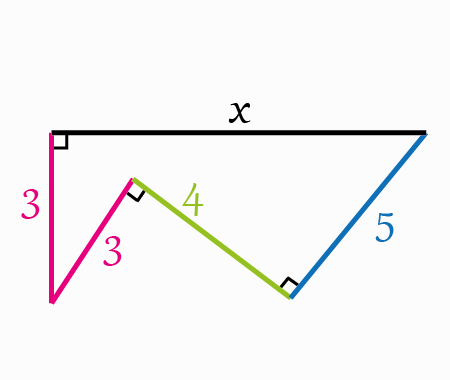
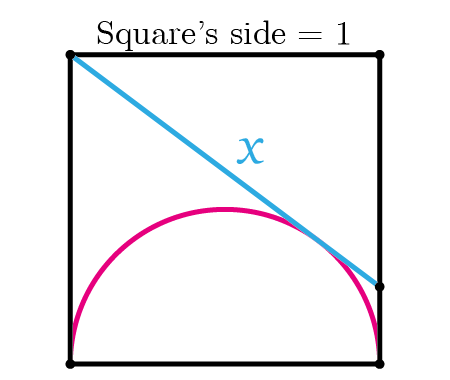
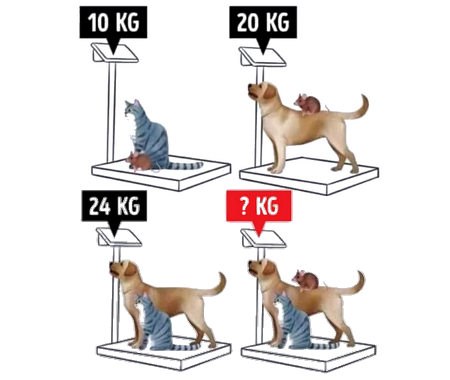
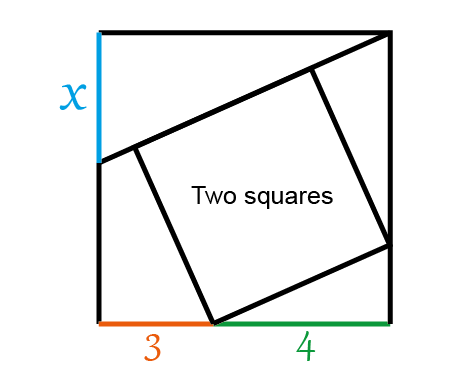
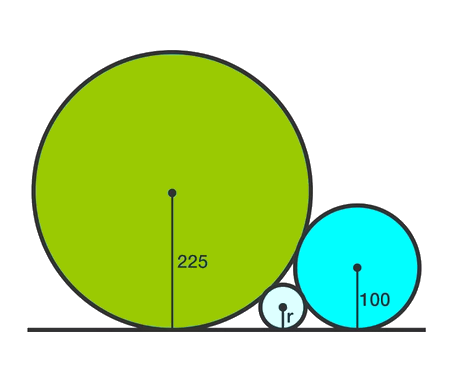
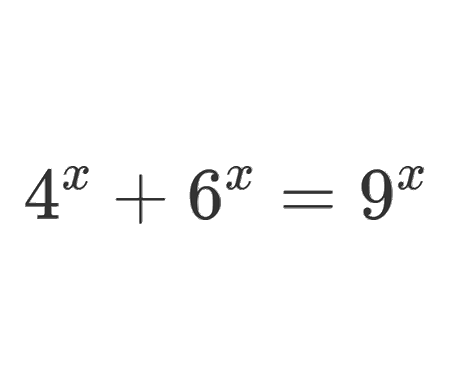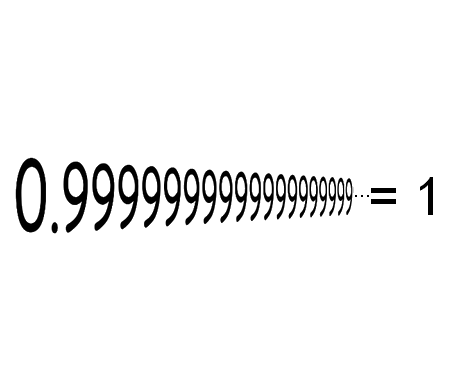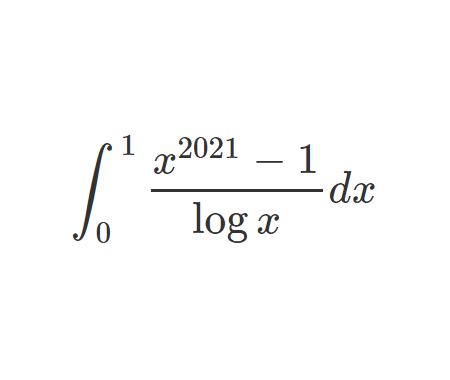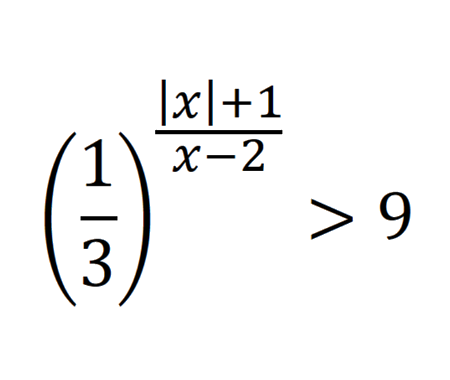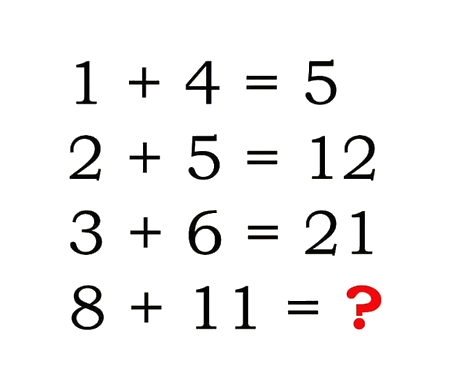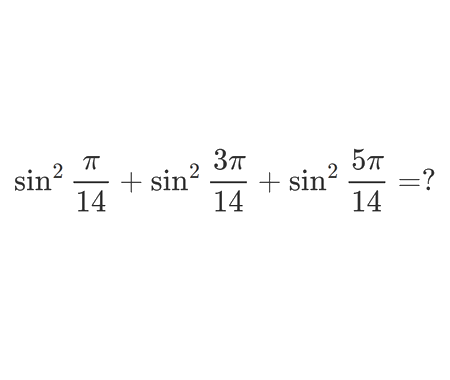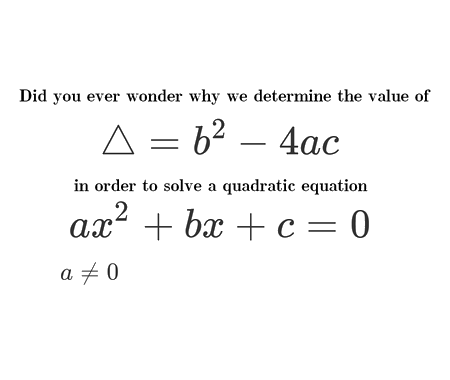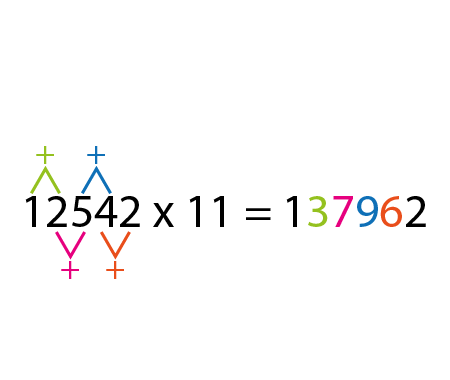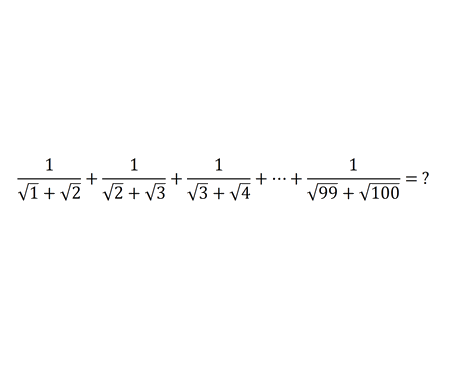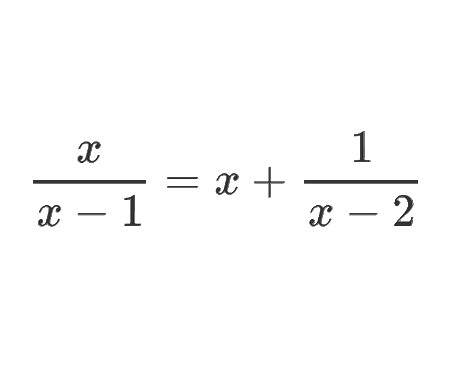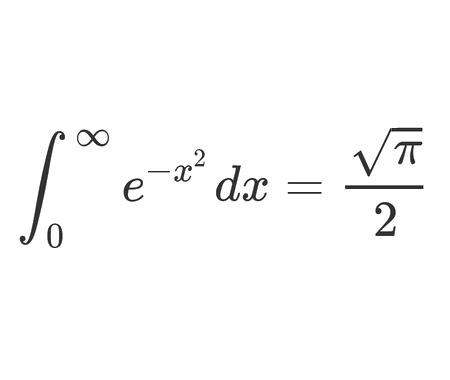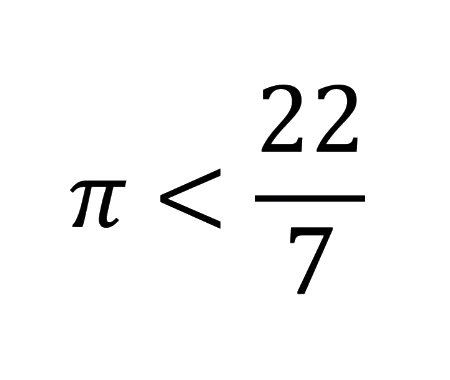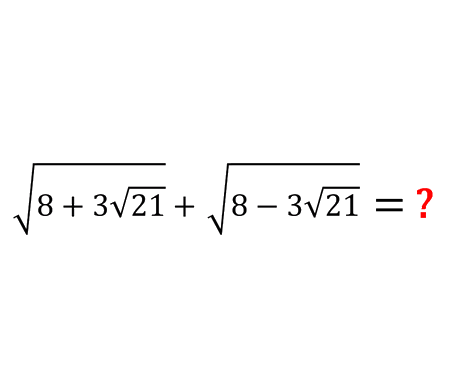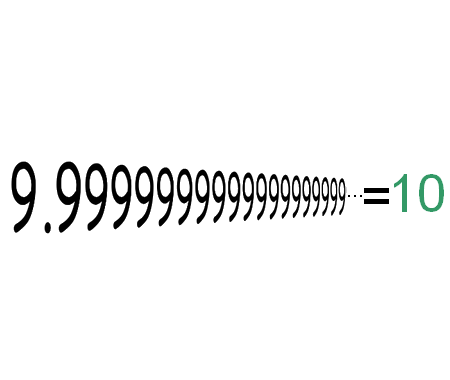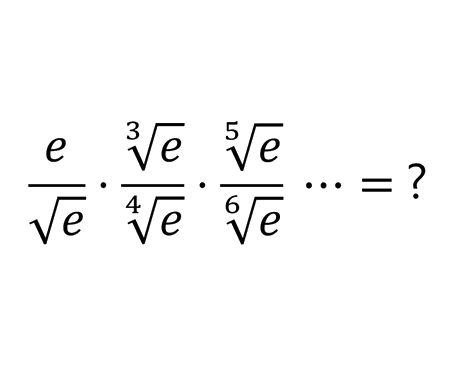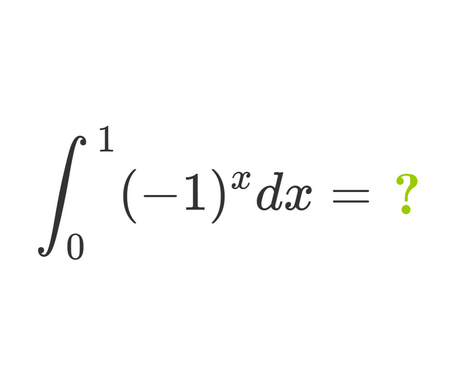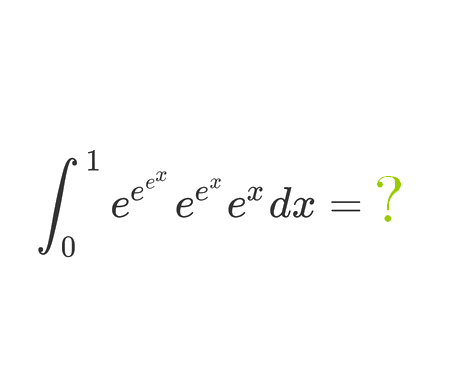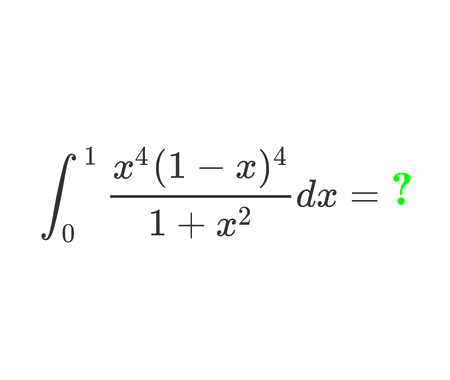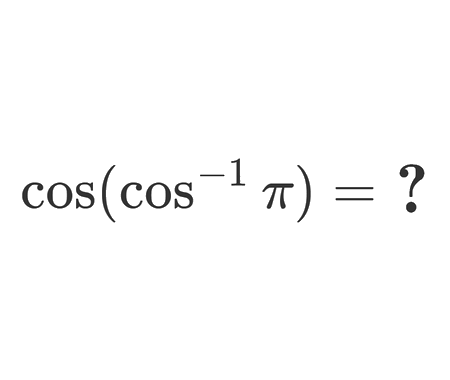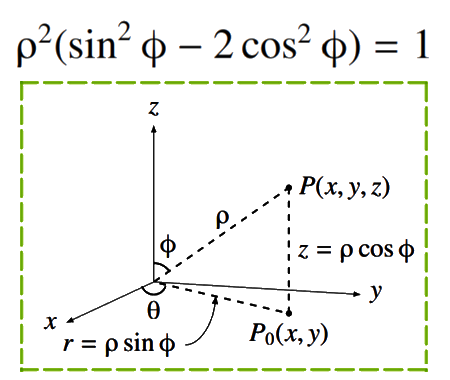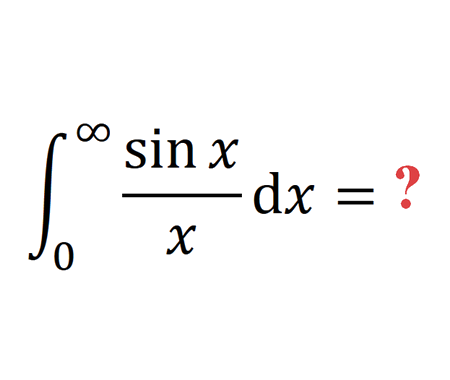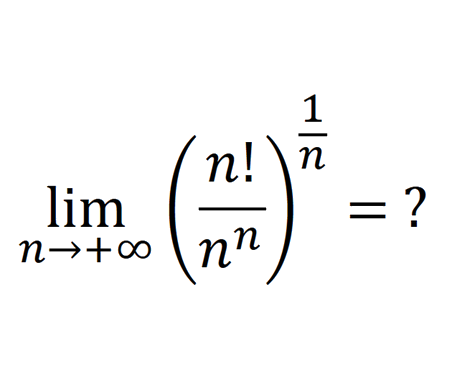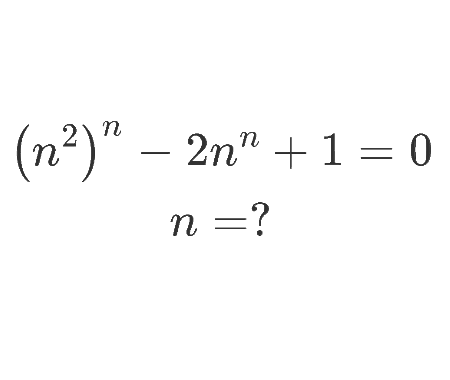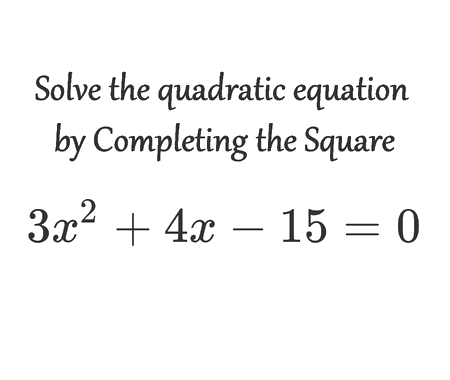Solution : Solve the Quadratic Equation by Completing the Square

Solve the quadratic equation by Completing the Square

Home -> Solved problems -> Solve the quadratic equation by Completing the Square

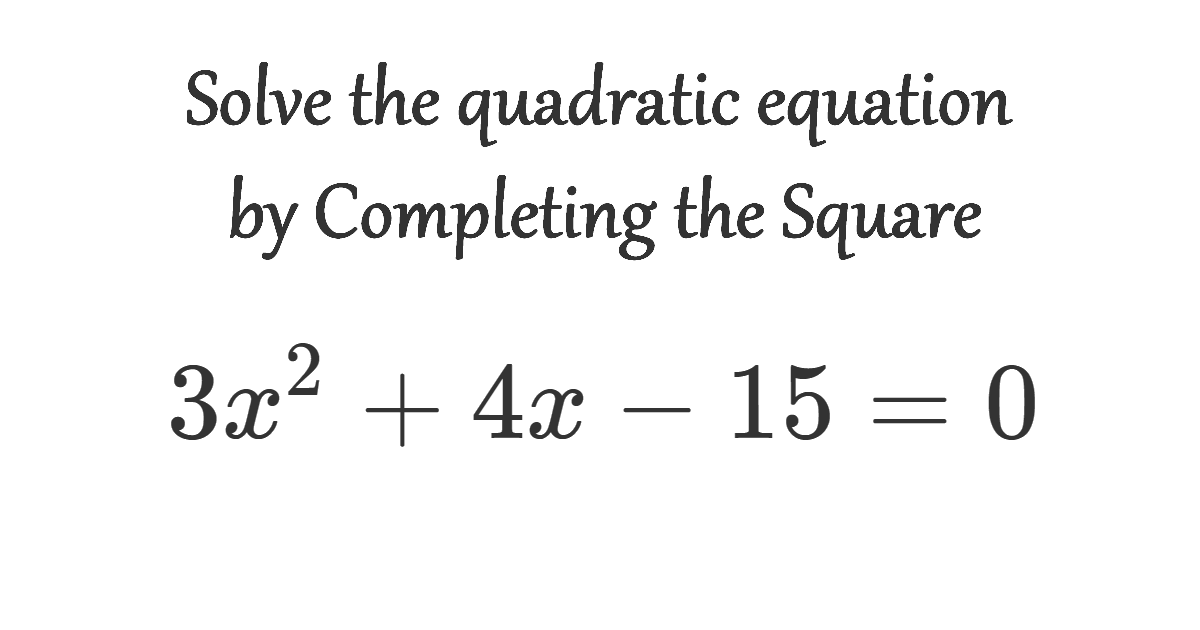
Solution

In this page we demonstrate how to solve a quadratic equation using the completing the square method.
This classical technique rewrites a general form ax² + bx + c = 0 as a perfect square, which simplifies solving for x, even when roots are irrational or complex. :contentReference[oaicite:1]{index=1}
The method also reveals important properties — for example, the vertex of the parabola defined by the quadratic — and forms the basis for the general quadratic formula. :contentReference[oaicite:2]{index=2}
Below, you will see a clear, step-by-step worked example that leads to the full solutions of the equation.

\[\begin{aligned} &3 x^2+4 x-15=0 \\\\ &x^2+\frac{4}{3} x-5=0 \\\\ &x^2+2\left(\frac{2}{3}\right) x+\left(\frac{2}{3}\right)^2-\left(\frac{2}{3}\right)^2-5=0 \\\\ &\left(x+\frac{2}{3}\right)^2=5+\frac{4}{9} \\\\ &\left(x+\frac{2}{3}\right)^2=\frac{45}{9}+\frac{4}{9} \\\\ &\left(x+\frac{2}{3}\right)^2=\frac{49}{9} \\\\ &x+\frac{2}{3}=\pm \frac{7}{3} \\\\ &x=\pm \frac{7}{3}-\frac{2}{3} \\\\ &x=\frac{7}{3}-\frac{2}{3} \text { or } x=\frac{-7}{3}-\frac{2}{3} \\\\ &x=\frac{5}{3} \text { or } x=-3 \end{aligned}\]

\[\text {Thus, the solution set}=\left\{-3, \frac{5}{3}\right\}\]

By completing the square, we transformed the quadratic equation into a perfect square trinomial and solved precisely for x.
This method is versatile: it works for any quadratic (even when roots are irrational or complex), and reveals more than just the roots — it also gives insight into the parabola’s vertex and its symmetry.
Remember that the key steps are: normalizing the coefficient of x² to 1 (if needed), moving the constant, adding \((b/2a)^2\) appropriately, then solving the resulting equation.
For more algebraic problems and solutions, feel free to browse our Solved Exercises section.

Home -> Solved problems -> Solve the quadratic equation by Completing the Square

Every problem you tackle makes you smarter.

↓ Scroll down for more maths problems↓

How Tall Is The Table ?

How far apart are the poles ?

Determine the square's side \(x\)

Find the volume of the interior of the kiln

Solve the equation for real values of \(x\)

Find the equation of the curve formed by a cable suspended between two points at the same height

Why 0.9999999...=1

Calculate the integral

Error to avoid that leads to:

What's the problem ?

Explain your answer without using calculator

Calculate the sum of areas of the three squares

What values of \(x\) satisfy this inequality

Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x} \) has a curvilinear asymptote \(y=x^{2}+2 x+3\)

Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?

Only one in 1000 can solve this math problem

Calculate the following

Find the limit of width and height ratio

Is \(\pi\) an irrational number ?

Solve for \(x \in \mathbb{R}\)

Prove that \(e\) is an irrational number

Prove that

Challenging problem

Solve the equation for \(x \in \mathbb{R}\)

Calculate the following limit

Determine the angle \(x\)

Find the derivative of \(y\) with respect to \(x\)

Prove Wallis Product Using Integration

Calculate the radius R

Calculate the volume of Torus using cylindrical shells

Find the derivative of exponential \(x\) from first principles

Find the volume of the square pyramid as a function of \(a\) and \(H\) by slicing method.

Prove that \[\lim_{x \rightarrow 0}\frac{\sin x}{x}=1\]

Prove that

Calculate the half derivative of \(x\)

Find out what is a discriminant of a quadratic equation.

Calculate the rectangle's area

Infinitely nested radicals

Determine the square's side \(x\)

Wonderful math fact: 12542 x 11 = 137962

Calculate the sum

What is the new distance between the two circles ?

Solve the equation for \(x\epsilon\mathbb{R}\)

Calculate the area of the Squid Game diagram blue part

Calculate the limit

Find the infinite sum

Calculate the integral

Prove that

Can we set up this tent ?

Find the value of \(h\)

Is the walk possible?

Find the length of the black segment

Prove that pi is less than 22/7

Find the value of \(x\)

Amazing !

Prove that

What is the weight of all animals ?

Determine the length \(x\) of the blue segment

if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?

What is the value of the following infinite product?

Which object weighs the same as the four squares?

What is \((-1)^{\pi}\) equal to?

Can you solve it?

Great Math Problem

Calculate the integral \(\int_{0}^{1}(-1)^{x} d x\)

Find the general term of the sequence

Find the radius of the blue circles

Determine the area of the green square

Find the area of the square

Calculate the integral

Calculate

What is the radius of the smallest circle ?

Find the Cartesian equation of the surface

Calculate the integral

Calculate the limit

Can you solve this ?

Solve the quintic equation for real \(x\)

How many students study no language ?

Probability of seeing a car in 10 minutes

What is the number of where the car stands ?

What is the value of \(x\) ?

Prove that

Is it possible to solve for \(x\) so that \(ln(x)\), \(ln(2x)\), and \(ln(3x)\) form a right triangle?

How many times will circle A revolve around itself in total ?

Find the distance \(BC\)

Solve for a^6, a : positive number

Solve the quadratic equation by Completing the Square