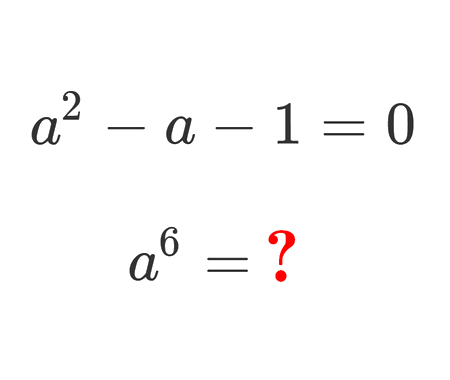Solve for a^6
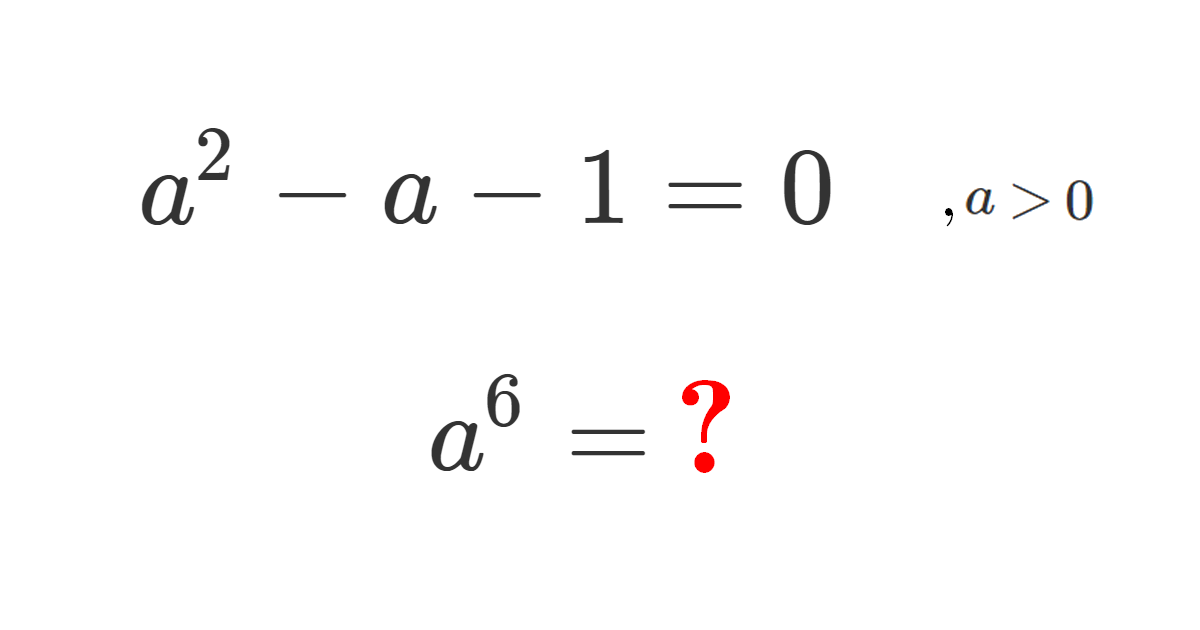
Solution
In this problem, we start from the quadratic equation a² − a − 1 = 0, and we assume a is the positive root.
Instead of computing a⁶ directly, we use algebraic identities and expansions to express a⁶ in terms of simpler expressions, which simplifies the calculation.
This approach highlights the power of algebraic manipulation and avoids approximations — the result is exact and elegant.
By combining the properties of the quadratic equation and binomial expansion, we showed that
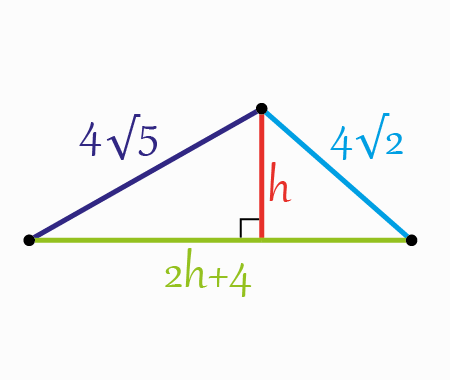
a⁶ = 9 + 4√5 for the positive root a of a² − a − 1 = 0.
This demonstrates how higher-power expressions can sometimes be reduced to simple forms without approximations.
Such methods are useful in algebra and number theory whenever you have an algebraic equation defining a base that you raise to a large power.
For more similar problems and algebraic reasoning, explore our Solved Exercises section.