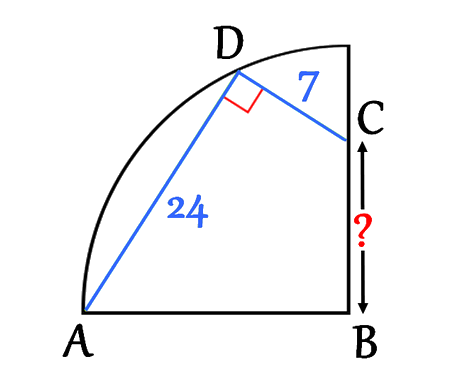
Find the distance BC, quarter circle
Home -> Solved problems -> Find the distance BC, quarter circle
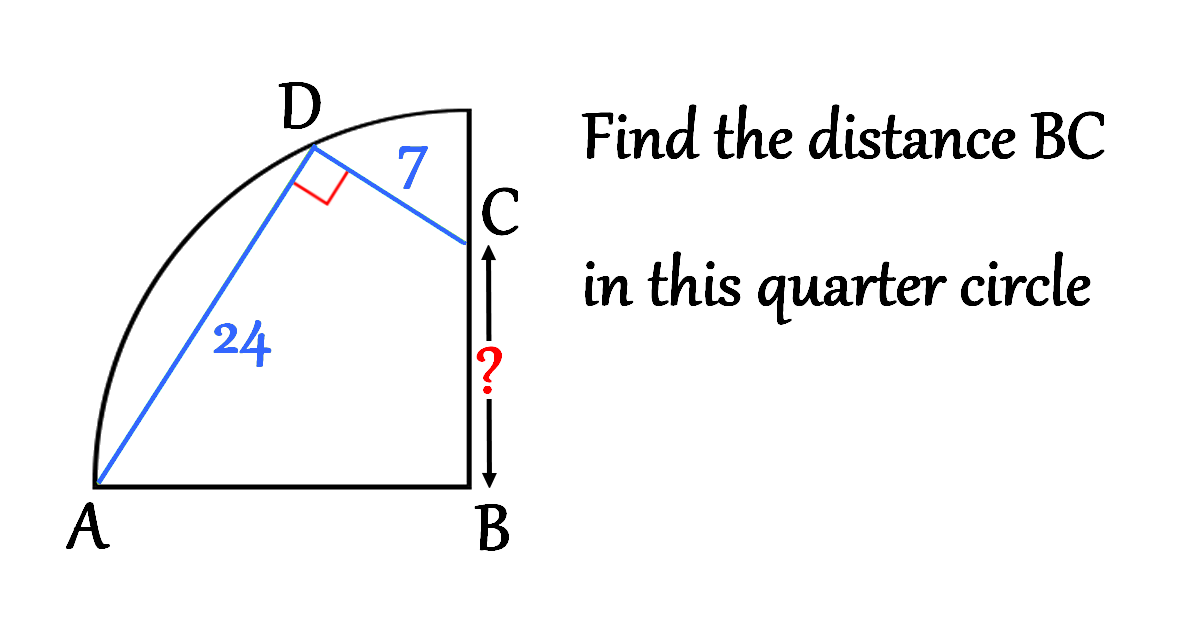
Solution
We have a right angle at the point \(D\), thus the line \(CD\) can be extended to a point \(E\) such that \(AE\) is a diameter of the circle like it is shown in the next figure
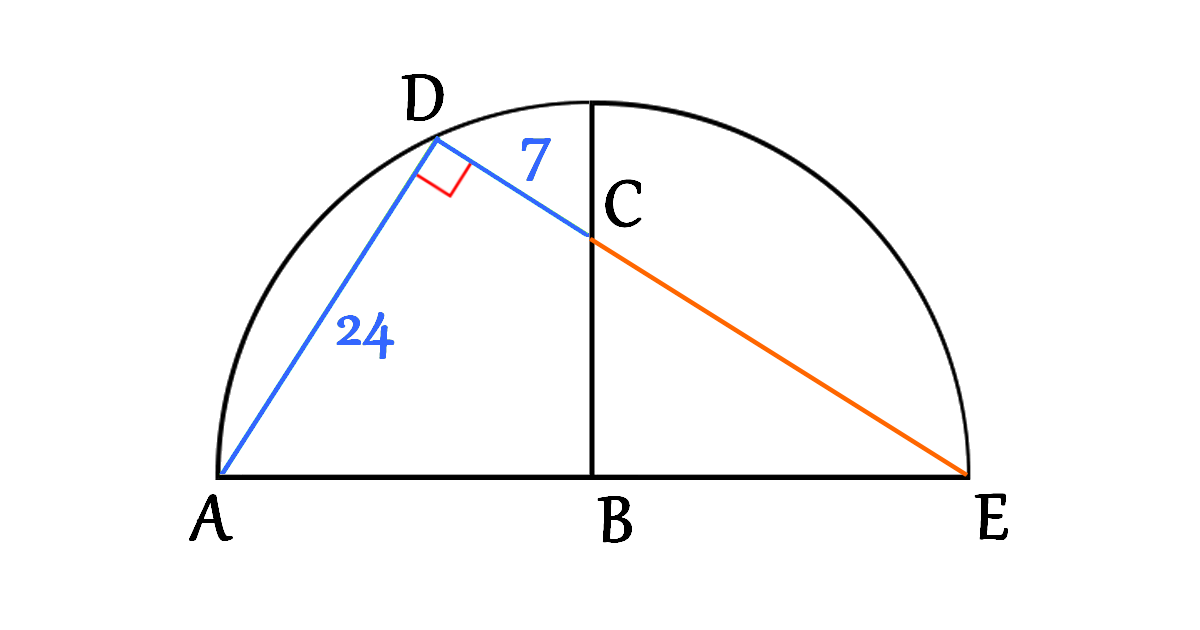
Now, let’s connect the two points \(A\) and \(C\) and focus on the triangle \(\triangle ADC\)
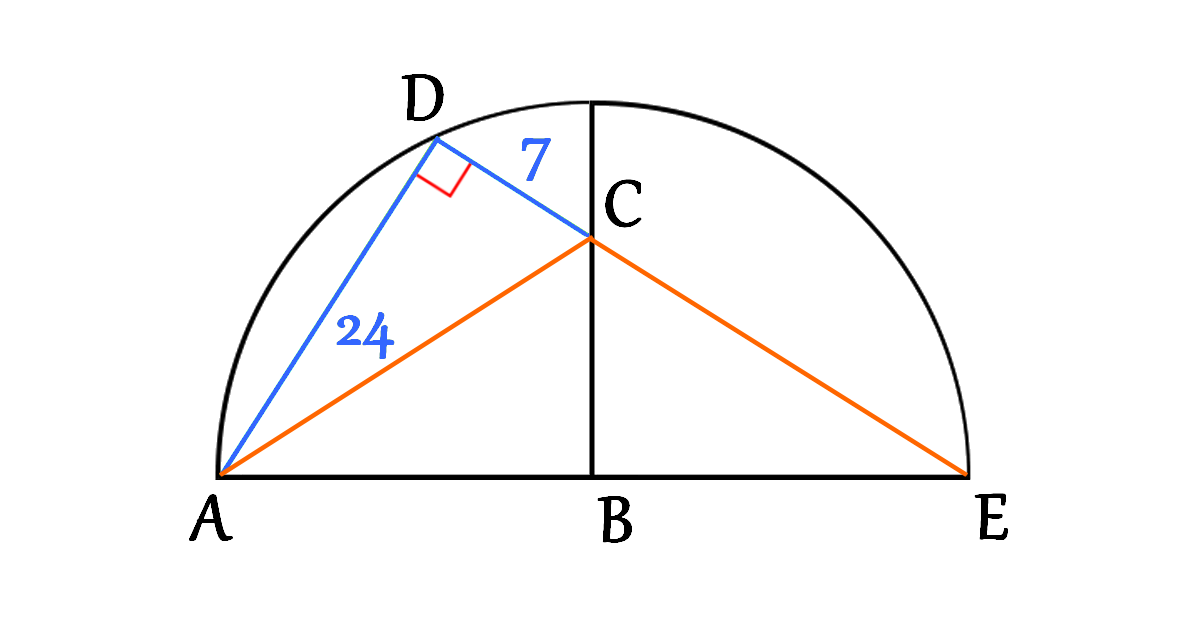
Using Pythagorean theorem
\[\begin{aligned}
A C^{2} &=A D^{2}+D C^{2} \\\\
A C^{2} &=24^{2}+7^{2} \\\\
&=576+49 \\\\
&=625 \\\\
A C &=25
\end{aligned}\]
The triangles \(\triangle ABC\) and \(\triangle EBC\) are congruent triangles, therefore \[CE=AC=25\]
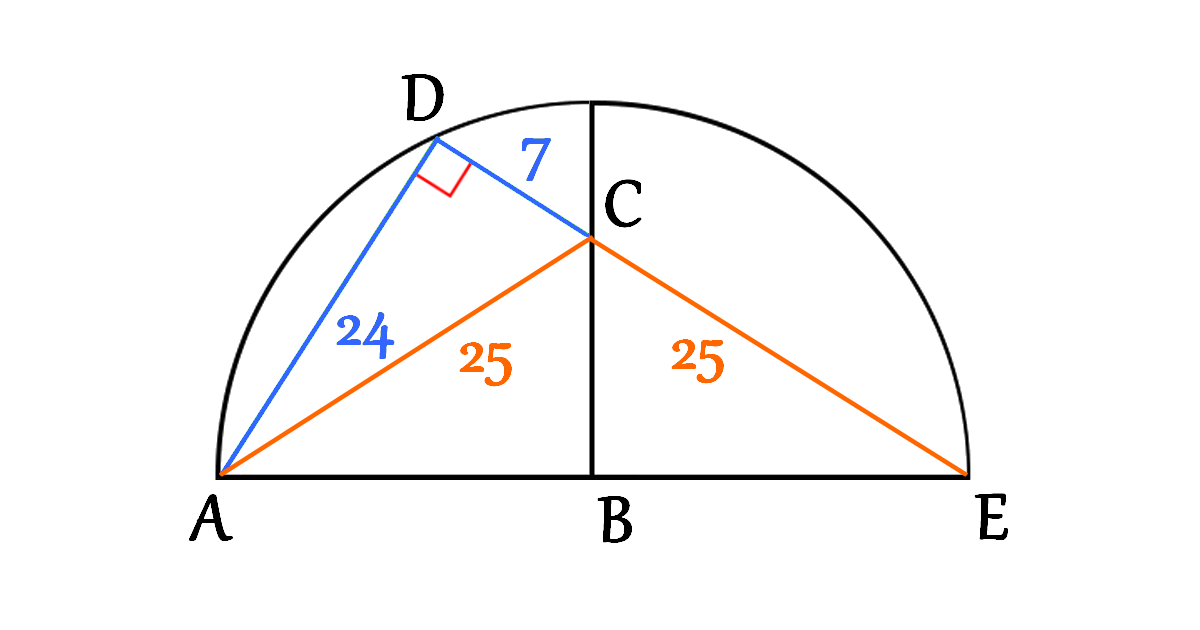
\[\begin{aligned}
&D E=D C+C E \\\\
&D E=7+25 \\\\
&D E=32
\end{aligned}\]
Let’s focus on the triangle \(\triangle ADE\) (Right triangle)
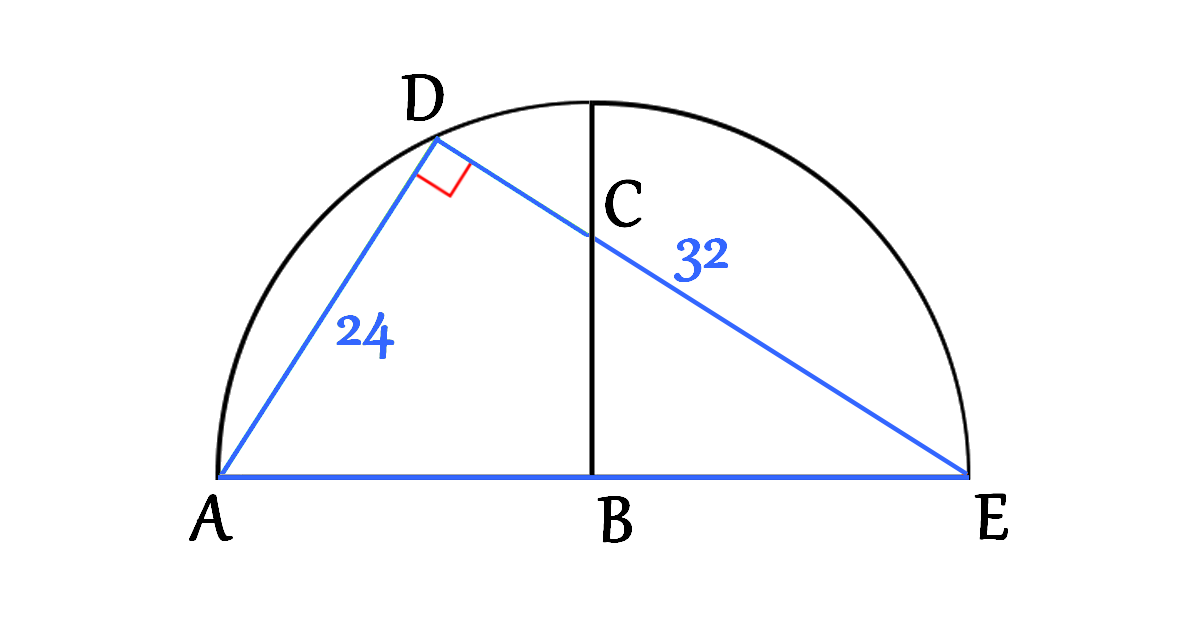
\[\begin{aligned}
A E^{2} &=A D^{2}+D E^{2} \\\\
&=24^{2}+32^{2} \\\\
&=576+1024 \\\\
&=1600 \\\\
A E &=40
\end{aligned}\]
Let’s focus on the triangle \(\triangle BEC\) (Right triangle)
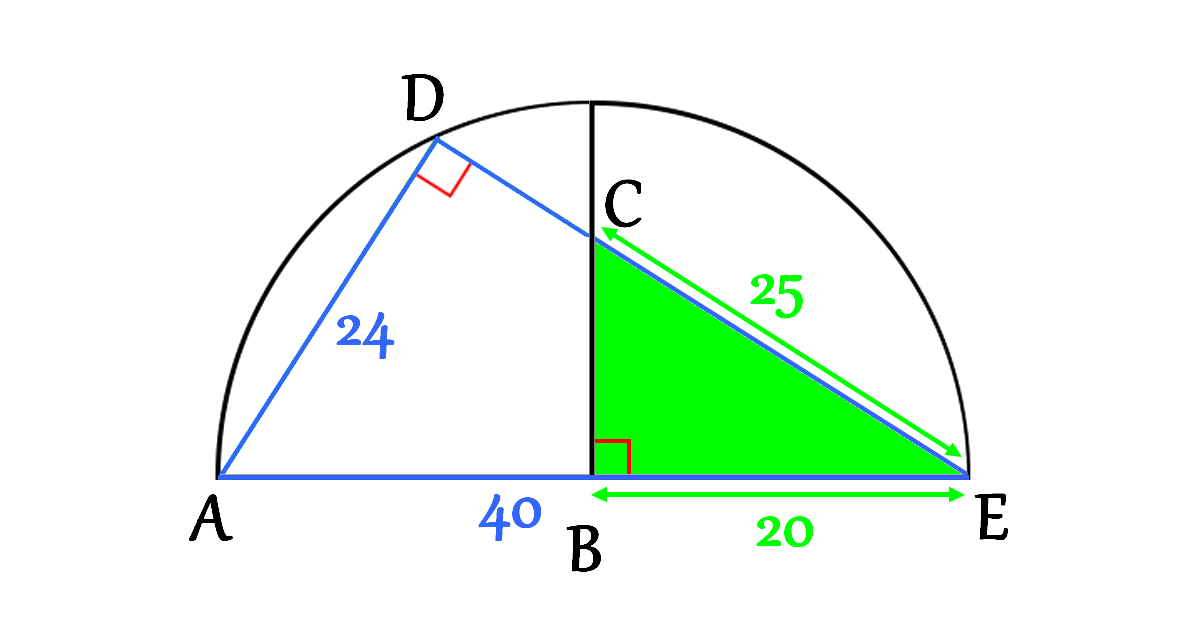
\[\begin{aligned}
C E^{2} &=B C^{2}+B E^{2} \\\\
B C^{2} &=C E^{2}-B E^{2} \\\\
&=25^{2}-20^{2} \\\\
&=625-400 \\\\
&=225 \\\\
B C &=15
\end{aligned}\]
Home -> Solved problems -> Find the distance BC, quarter circle
Every problem you tackle makes you smarter.
↓ Scroll down for more maths problems↓
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?
