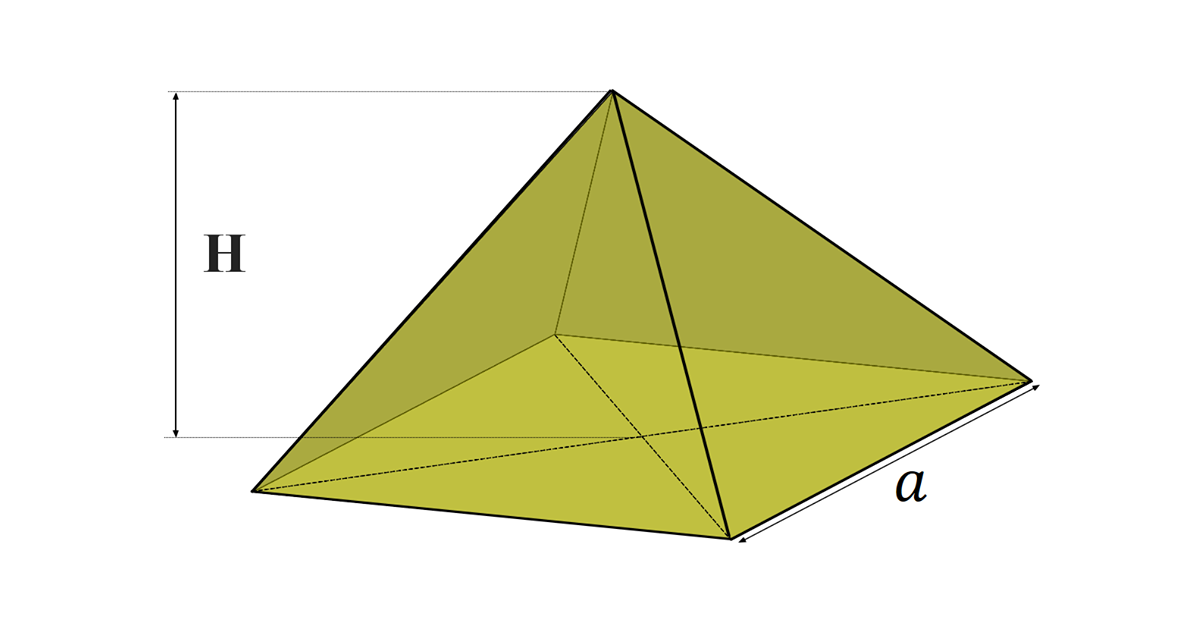
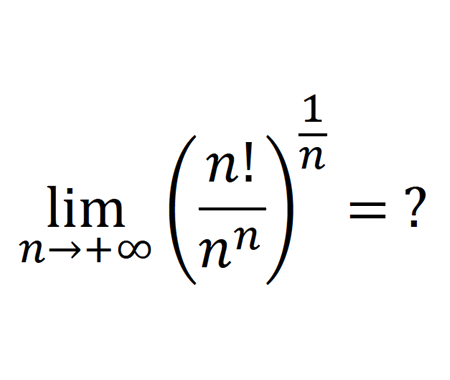Find the square pyramid volume as a function of \(a\) and \(H\) by slicing method
Home -> Solved problems -> Volume square pyramid
Solution
The first step is to find the volume of one slice of the pyramid. The slice is considered as a square cuboid with side \(x\) and infinitesimally small height \(\text{d}h\) as shown in blue in the figure below, so we can affirm that the slice’s volume is \(\text{d}v=x^{2}\text{d}h\). Now to continue we need to find a relationship between \(x\) and \(h\) before applying integration . \(h\) is the distance between the cuboid and the square base of the pyramid. So to do that, we use Thales‘s theorem in the triangle with the orange line segments.
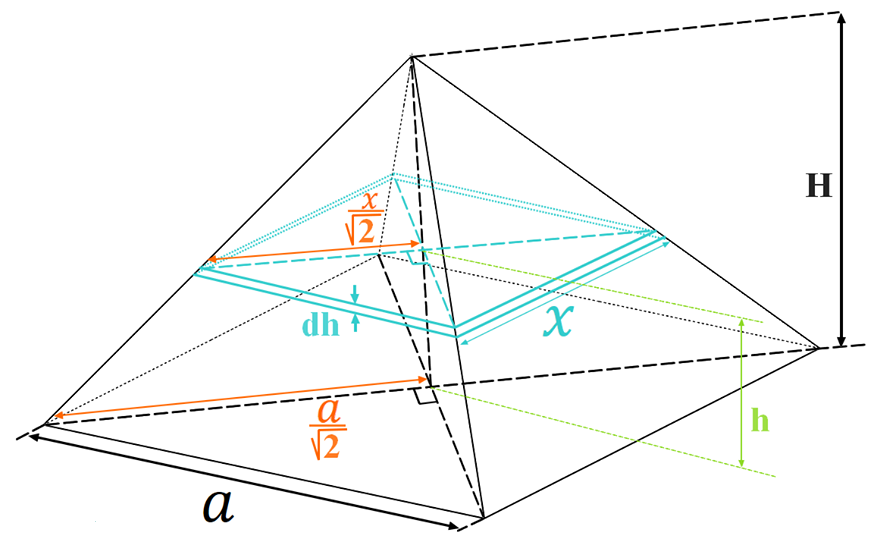
We get,\[\frac{\frac{x}{\sqrt{2}}}{\frac{a}{\sqrt{2}}}=\frac{H-h}{H}\]\[\frac{x}{a}=\frac{H-h}{H}\]\[ x=a(\frac{H-h}{H})\]
After finding a relationship between \(x\) and \(h\) we can calculate the pyramid volume by applying integral between \(0\) and \(H\). \(a\) and \(H\) are constants. \[\text{d}v=x^{2}\text{d}h\]\[=(a(\frac{H-h}{H}))^{2}\text{d}h\]\[v=\int_{0}^{H} (a(\frac{H-h}{H}))^{2}\text{d}h\]\[=(\frac{a}{H})^{2}\int_{0}^{H} (H-h)^{2}\text{d}h\]\[=(\frac{a}{H})^{2}(-\frac{(H-h)^{3}}{3})|_0^H\]\[=(\frac{a}{H})^{2}(-\frac{(H-H)^{3}}{3})-(\frac{a}{H})^{2}(-\frac{(H-0)^{3}}{3})\]\[=-(\frac{a}{H})^{2}(-\frac{H^{3}}{3})\]\[=\frac{a^{2}H^{3}}{3H^{2}}\]\[=\frac{1}{3}a^{2}H\]
Home -> Solved problems -> Volume square pyramid
Every problem you tackle makes you smarter.
↓ Scroll down for more maths problems↓
↓ ↓
↓ ↓
↓ ↓
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
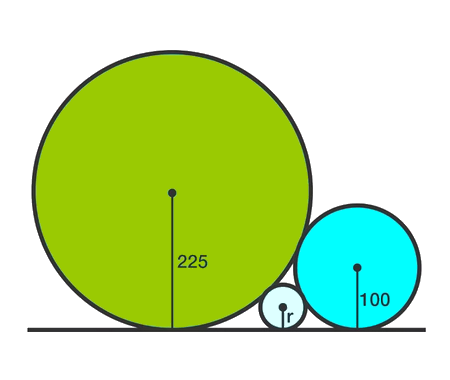
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
Home -> Solved problems -> Volume square pyramid