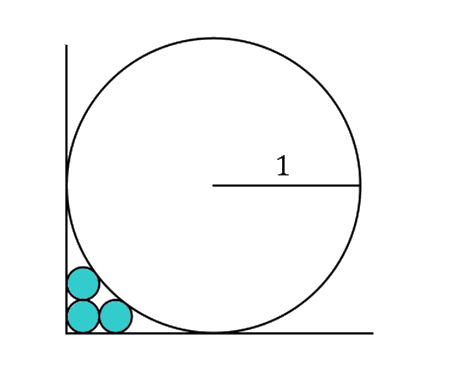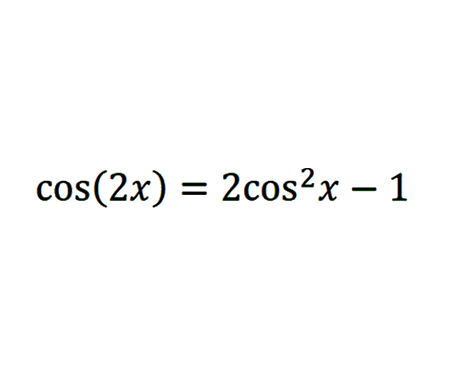Prove that cos(2x)=2cos²x-1
Home -> Solved problems -> Prove that cos(2x)=2cos²x-1
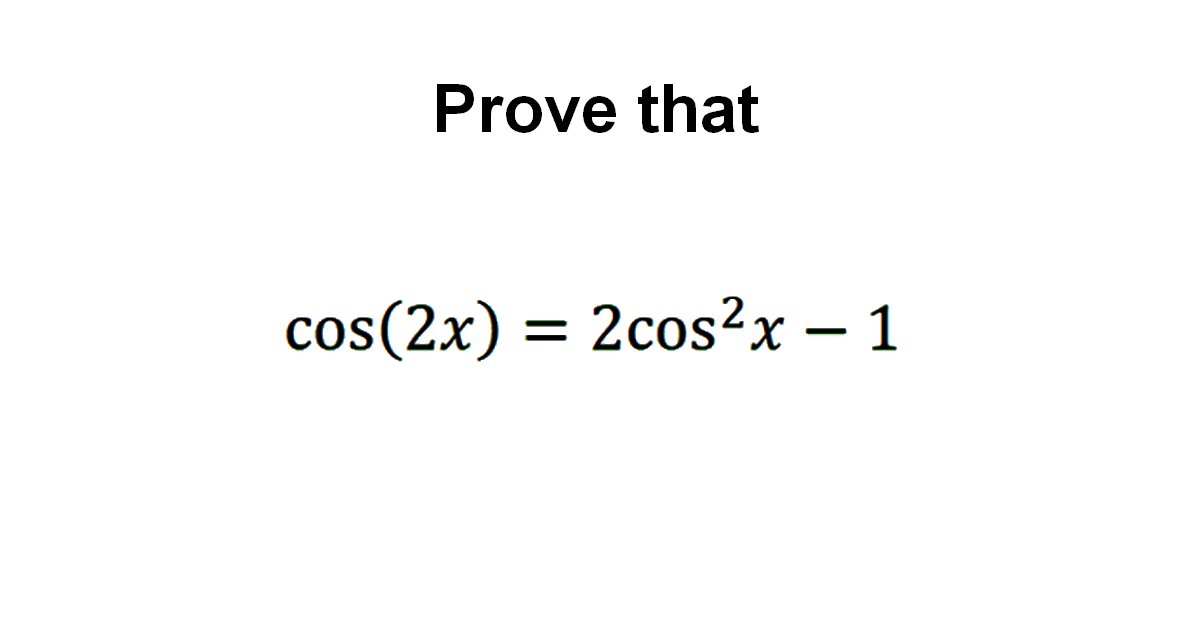
Solution
\[\begin{aligned}
\cos (2 x) &=\frac{e^{2 i x}+e^{-2 i x}}{2}=\frac{\left(e^{i x}\right)^{2}+\left(e^{-i x}\right)^{2}}{2} \\\\
&=\frac{(\cos x+i \sin x)^{2}+(\cos x-i \sin x)^{2}}{2} \\\\
&=\frac{\cos ^{2} x+2 i \cos x \sin x-\sin ^{2} x+\cos ^{2} x-2 i \cos x \sin x-\sin ^{2} x}{2} \\\\
&=\frac{\cos ^{2} x-\sin ^{2} x+\cos ^{2} x-\sin ^{2} x}{2}=\frac{2 \cos ^{2} x-2 \sin ^{2} x}{2} \\\\
&=\cos ^{2} x-\sin ^{2} x=\cos ^{2} x-\left(1-\cos ^{2} x\right) \\\\
&=\cos ^{2} x-1+\cos ^{2} x \\\\
&=2 \cos ^{2} x-1
\end{aligned}\]
Home -> Solved problems -> Prove that cos(2x)=2cos²x-1
Every problem you tackle makes you smarter.
↓ Scroll down for more maths problems↓
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
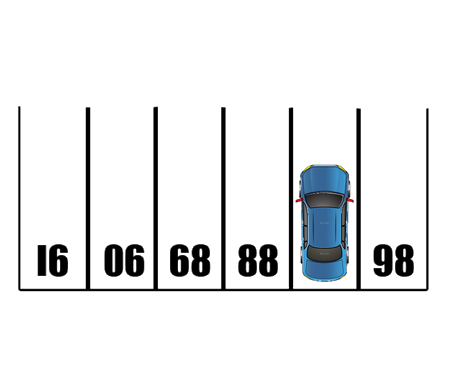
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?