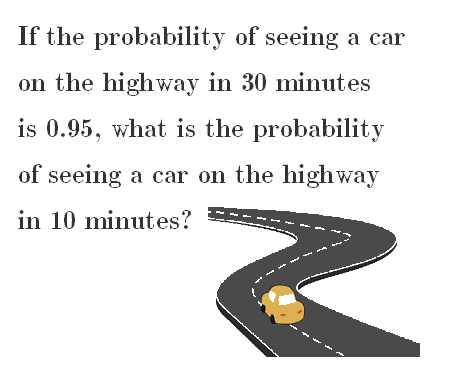
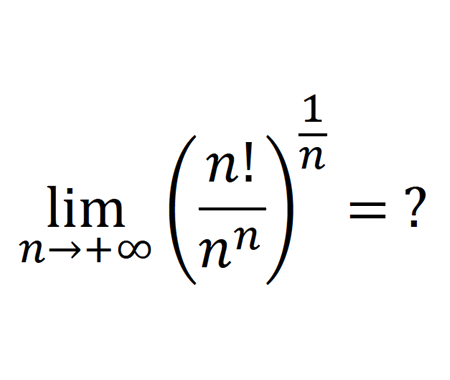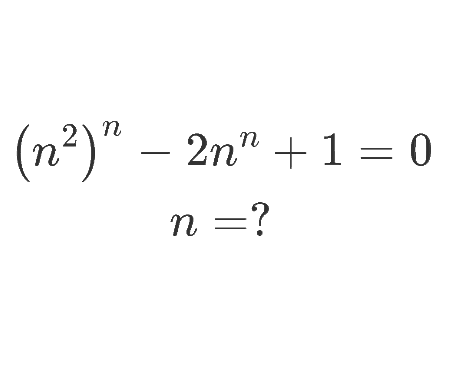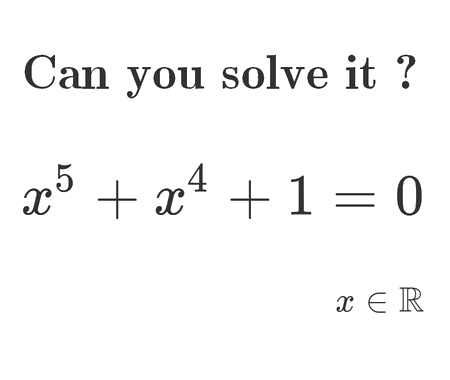Probability of seeing a car in 10 minutes
Solution
Let’s consider every \(10\) minutes interval like a coin flip. Let \(p\) the probability of not seeing a car in \(10\) minutes.
Let’s find the probability of not seeing a car in \(20\) minutes. It’s like repeating twice the event not seeing a car in \(10\) minutes.
\(Pb\)(no cars in \(20\)) = \(Pb\)(no cars in \(10\)) \(Pb\)(no cars in \(10\))
\(Pb\)(no cars in \(20\)) = \(p\)(\(p\))
\(Pb\)(no cars in \(20\)) = \(p^{2}\)
Now, let’s find the probability of the event not seeing a car in \(30\) minutes. It’s the probability of the event not seeing a car in \(20\) minutes, followed by the event not seeing a car in \(10\) minutes.
\(Pb\)(no cars in \(30\)) = \(Pb\)(no cars in \(20\)) \(Pb\)(no cars in \(10\))
\(Pb\)(no cars in \(30\)) = \(p^{2}\)(\(p\))
\(Pb\)(no cars in \(30\)) = \(p^{3}\)
we can directly calculate
\(Pb\)(no cars in \(30\)) = \(Pb\)(no cars in \(10\)) \(Pb\)(no cars in \(10\)) \(Pb\)(no cars in \(10\))= \(p^{3}\)
Let’s continue, the probability of seeing at least \(1\) car in \(30\) minutes is the complement event of seeing no cars in \(30\) minutes.
\(Pb\)(car in \(30\)) = \(1\) – \(Pb\)(no cars in \(30\))
\(Pb\)(car in \(30\)) = \(1\) – \(p^{3}\)
This is equal to \(0.95\). We get an equation to solve for \(p\) :
\(1\) – \(p^{3}\) = \(0.95\)
\(p^{3}\) = \(0.05\)
\(p\) = \(0.05^{\frac{1}{3}}
\) \(\approx
\) \(0.368
\)
The probability of seeing at least \(1\) car in \(10\) minutes is the complement event of seeing no cars in \(10\) minutes.
\(Pb\)(car in \(10\)) = \(1\) – \(Pb\)(no cars in \(10\))
\(Pb\)(car in \(10\)) = \(1\) – \(p\)
\(Pb\)(car in \(10\)) \(\approx
\) \(0.632
\)
Finally, the answer is approximately \(63\) percent.
Every problem you tackle makes you smarter.
↓ Scroll down for more maths problems↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
