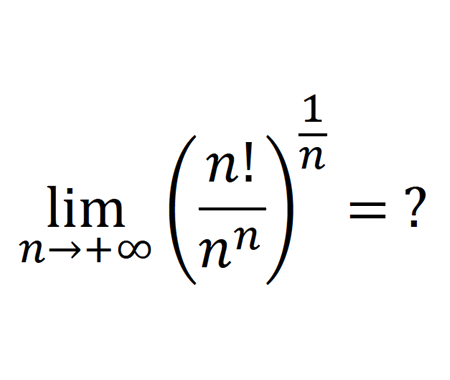What is the value of the circle's radius \(R\) ? (circle and rectangle in square )
Home -> Solved problems -> Calculate the radius R (circle and rectangle in square)
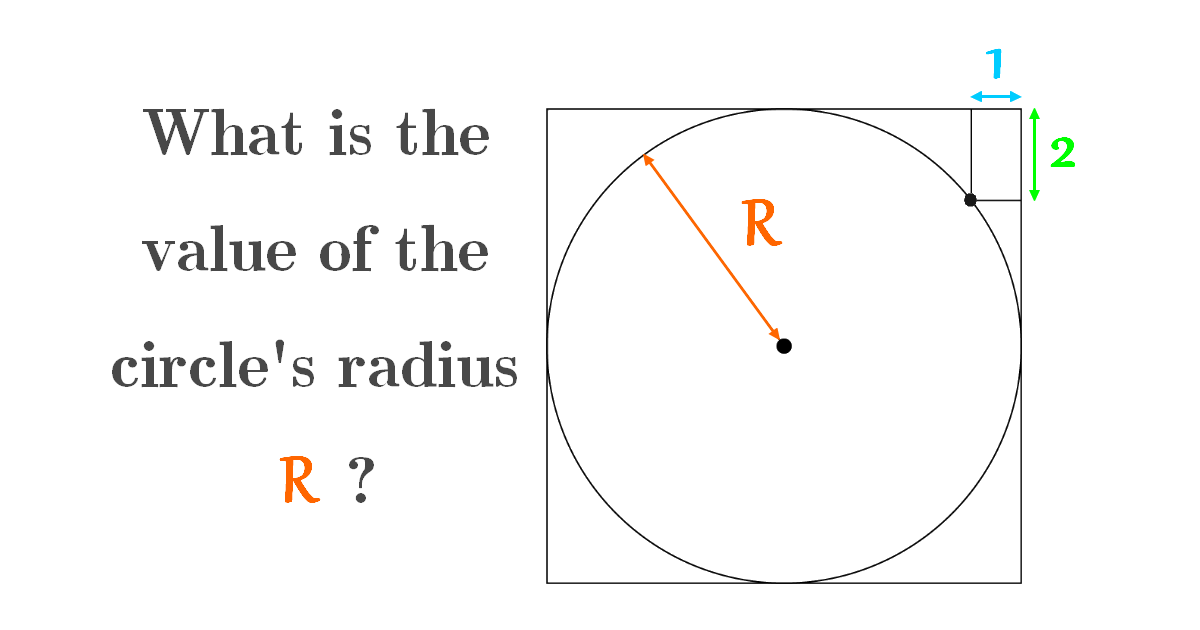
Solution
This proof explores the value of the radius R in a configuration of a circle and rectangle inside a square. Follow the steps below to see how R is calculated geometrically.
First, we identify the known sides of the square and rectangle. Next, we determine the relationship between the circle and rectangle. Finally, we calculate the radius R using geometric properties.
To solve the problem, we simplify it by adding an angle \(x\) like it is shown in the next figure.
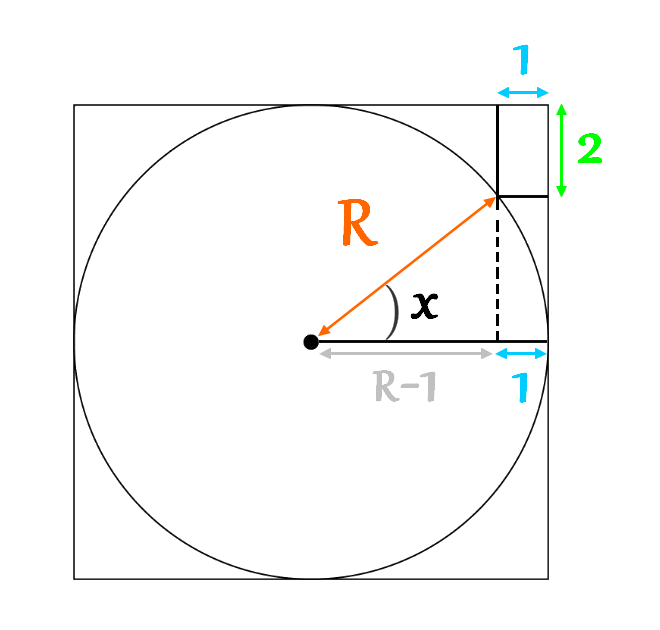
Now, let’s calculate:
\[
\cos x = \frac{R-1}{R}, \quad
\sin x = \frac{R-2}{R}
\]
\[
(\sin x)^2 + (\cos x)^2
= \left(\frac{R-2}{R}\right)^2 + \left(\frac{R-1}{R}\right)^2
= 1
\]
\[
\frac{R^2 – 4R + 4 + R^2 – 2R + 1}{R^2} = 1
\]
\[
2R^2 – 6R + 5 = R^2 \quad \Rightarrow \quad R^2 – 6R + 5 = 0
\]
\[
(R-1)(R-5) = 0
\]
The solution \(R=1\) is not accepted because \(\cos x \neq 0\). Therefore:
\[
\color{orange}{R=5}
\]
For more exercises and their detailed solutions, check out our Solved Exercises page.
Home -> Solved problems -> Calculate the radius R (circle and rectangle in square)
Every problem you tackle makes you smarter.
↓ Scroll down for more maths problems↓
↓ ↓
↓ ↓
↓ ↓
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
Home -> Solved problems -> Calculate the radius R (circle and rectangle in square)