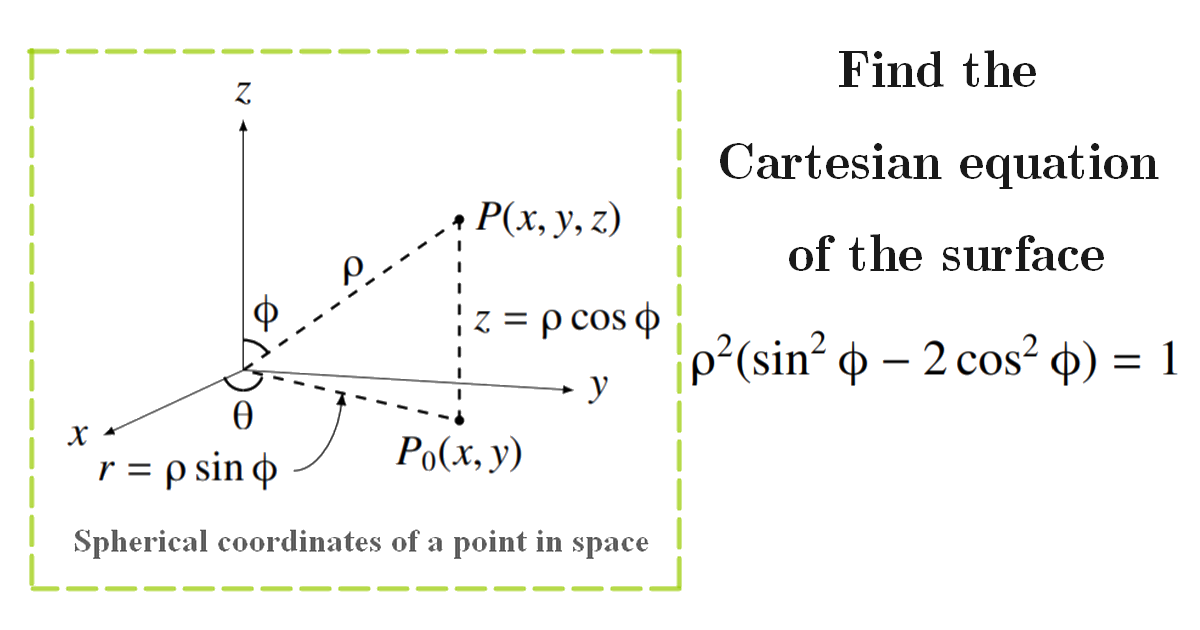
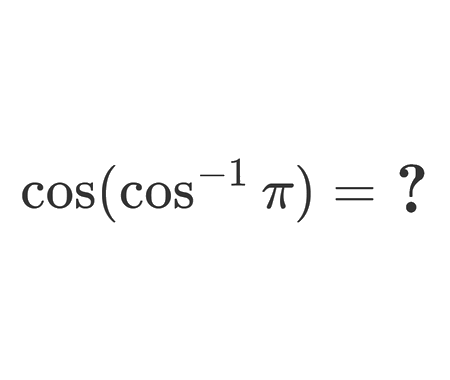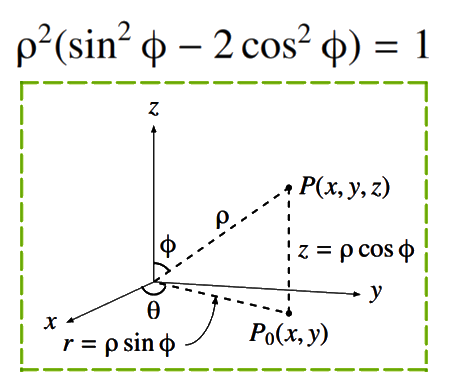Find the Cartesian equation of the surface \[\rho^{2}\left(\sin ^{2} \phi-2 \cos ^{2} \phi\right)=1 \]
Home -> Solved problems -> Find the Cartesian equation of the surface
Solution
Since
\[\begin{aligned}
&x^{2}+y^{2}=\rho^{2} \sin ^{2} \phi \cos ^{2} \theta+\rho^{2} \sin ^{2} \phi \sin ^{2} \theta\\\\&=\rho^{2} \sin ^{2} \phi
\end{aligned}\]
We have
\[\begin{aligned}
&\rho^{2} \sin ^{2} \phi-2 \rho^{2} \cos ^{2} \phi=1 \quad \\\\&\Longleftrightarrow \quad x^{2}+y^{2}-2 z^{2}=1
\end{aligned}\]
The last equation represents a surface known as ‘one-sheet hyperboloid’. The surface is represented in the next figure
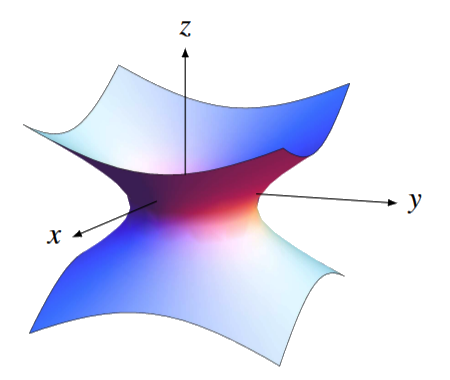
Hyperboloid : \(x^{2}+y^{2}-2 z^{2}=1\)
Home -> Solved problems -> Find the Cartesian equation of the surface
Every problem you tackle makes you smarter.
↓ Scroll down for more maths problems↓
↓ ↓
↓ ↓
↓ ↓
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
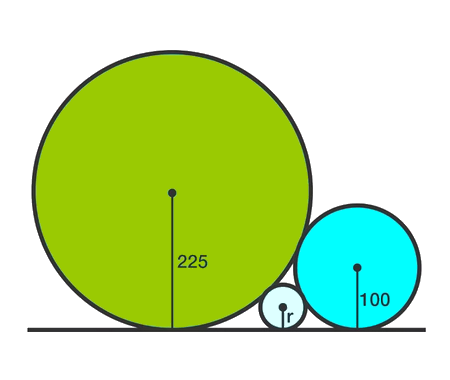
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
Home -> Solved problems -> Find the Cartesian equation of the surface