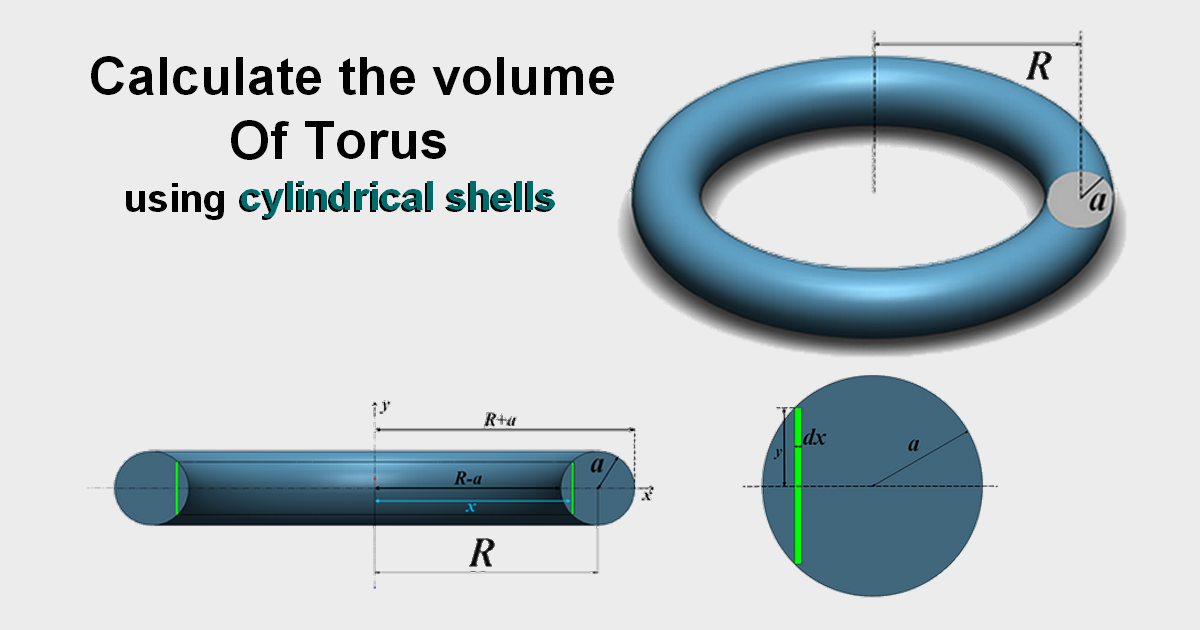
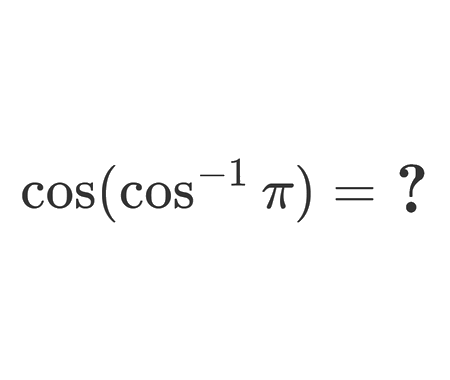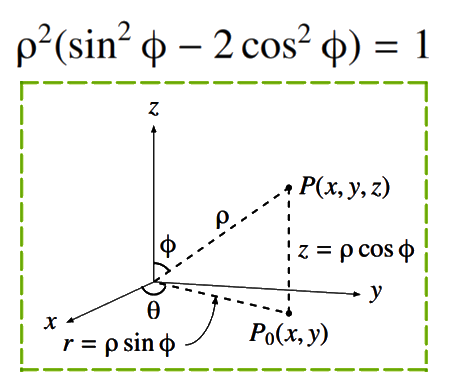Calculate the volume of Torus using cylindrical shells
Home -> Solved problems -> Volume of torus using cylindrical shells
Solution
To start, let’s talk a little bit about Torus. We get a Torus by revolving a circle in a 3D space around an axis which is in the same plane as the circle, like it is shown in the next figure
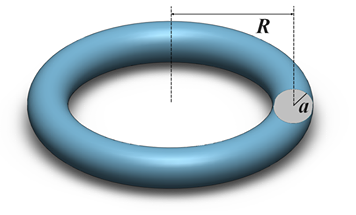
Now, let’s find out how to calculate the Torus volume. To do that we take the circle of radius \(a\) and center situated at a distance of \(R\) from the axis. We divide the circle into infinitesimal slices, and we consider only one slice of width \(\text{d}x\) and height \(2y\) like it is shown in \(\color{green} {green}\) in the next figure
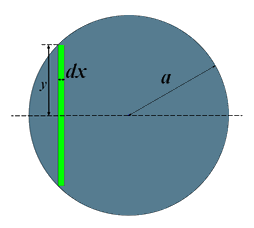
The idea is when we revolve the circle around the axis we get the Torus and when we revolve the green slice around the axis we get a cylindrical shell. The next figure explains that
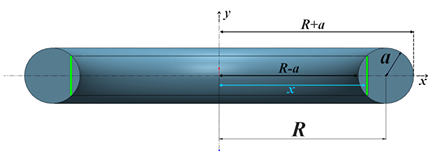
Now, we need to calculate the volume of the cylindrical shell. The origin of the coordinate system is a point of the axis like it is shown in the figure above. The equation of the circle is: \[\left(x-R\right)^{2}+y^{2}=a^{2}\Rightarrow y^{2}=a^{2}-\left(x-R\right)^{2}\] \[\Rightarrow|y|=\sqrt{a^{2}-\left(x-R\right)^{2}}\] If we want to work on the top part of the circle, then \(y\geq0\) therefore \[y=\sqrt{a^{2}-\left(x-R\right)^{2}}\] Let \(\text{d}s\) be the area of the circle slice, \[\text{d}s=\left(2y\right)\text{d}x\] Now, let’s considerate the next figure that shows a cylindrical shell obtained by revolving the circle slice about the axis by \(2\pi\)
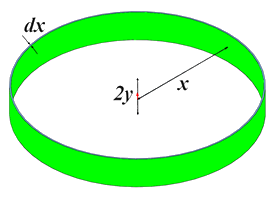
The circle slice is situated at a distance of \(x\) from the axis. Let \(\text{d}v\) be the volume of the cylindrical shell, thus \[\text{d}v=2\pi x\text{d}s\] \[=2\pi x\left(2y\right)\text{d}x\] \[=4\pi x \sqrt{a^{2}-\left(x-R\right)^{2}}\text{d}x\] For \(R-a\leq x\leq R+a\) \[v=\int_{R-a}^{R+a} 4\pi x \sqrt{a^{2}-\left(x-R\right)^{2}}\text{d}x\] Let’s change the variable of integration, let \[\sin\theta=\frac{x-R}{a}\Rightarrow x-R=a\sin\theta\] \[a^{2}-\left(x-R\right)^{2}=a^{2}\left(1-\left(\sin\theta\right)^{2}\right)=a^{2}\left(\cos\theta\right)^{2}\] When \(x=R-a\Leftrightarrow\theta=-\frac{\pi}{2}\) and when \(x=R+a\Leftrightarrow\theta=\frac{\pi}{2}\) \[\text{d}x=a\cos\theta\text{d}\theta\] And then let’s return to the integral \[v=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}4\pi\left(R+a\sin\theta\right)a\left(\cos\theta\right) a\left(\cos\theta\right)\text{d}\theta\] \[=4\pi a^{2}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\left(R\left(\cos\theta\right)^{2}+a\sin\theta\left(\cos\theta\right)^{2}\right)\text{d}\theta\] \[=4\pi a^{2}\left(\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}R\left(\cos\theta\right)^{2}\text{d}\theta+a\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sin\theta\left(\cos\theta\right)^{2}\text{d}\theta\right)\] \[=4\pi a^{2}\left(\frac{R}{2}\left(\frac{\sin2\theta}{2}+\theta\right)_\frac{-\pi}{2}^\frac{\pi}{2}-a\left(\frac{\left(\cos\theta\right)^{3}}{3}\right)_\frac{-\pi}{2}^\frac{\pi}{2}\right)\] \[=4\pi a^{2}\left(\frac{R}{2}\left(\frac{\sin\left(2\frac{\pi}{2}\right)}{2}+\frac{\pi}{2}-\frac{\sin\left(2\left(-\frac{\pi}{2}\right)\right)}{2}+\frac{\pi}{2}\right)-a\left(\frac{\left(\cos\frac{\pi}{2}\right)^{3}}{3}-\frac{\left(\cos\left(-\frac{\pi}{2}\right)\right)^{3}}{3}\right)\right)\] \[=4\pi a^{2}\left(\frac{R}{2}\pi\right)\] \[\large \color{olive} {v=2 \pi^{2}a^{2}R}\]
Home -> Solved problems -> Volume of torus using cylindrical shells
Every problem you tackle makes you smarter.
↓ Scroll down for more maths problems↓
↓ ↓
↓ ↓
↓ ↓
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
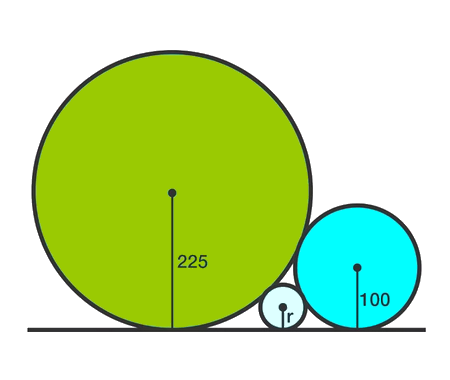
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
Home -> Solved problems -> Volume of torus using cylindrical shells