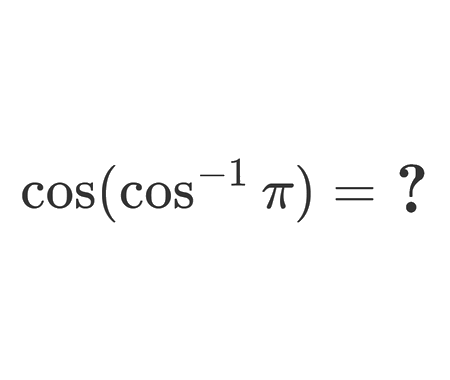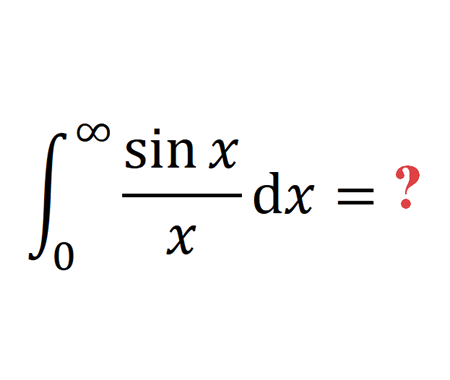Prove Stirling's formula
Home -> Solved problems -> Stirling’s formula
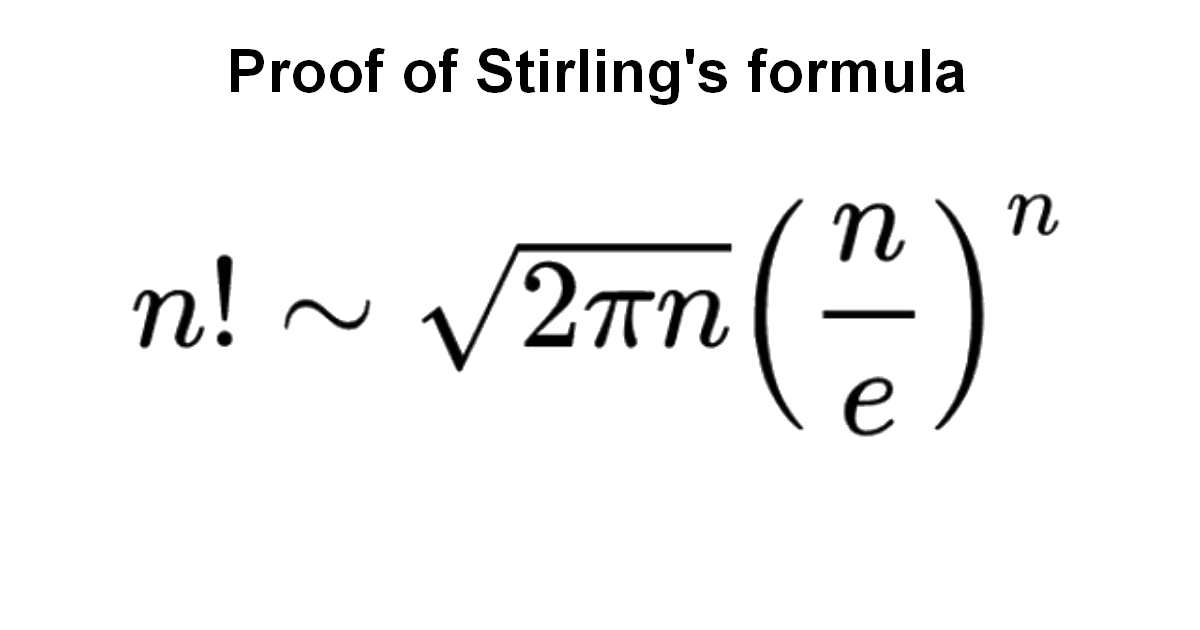
Solution
Stirling’s approximation is an important approximation for factorials. It is leading to accurate results even for small values of \(n\). It is named after James Stirling, though it was first stated by Abraham de Moivre.
First, we know that \(n!=1\cdot2\cdot\cdot\cdot n\). We take the \(\log\) of \(n!\) we get \[\log(n!)=\log(1)+\log(2)+\cdot\cdot\cdot+\log(n)\] The \(\log\) function is increasing on \((0,\infty)\), we get \[\int_{n-1}^{n}\log(x)\text{d}x<\log(n)<\int_{n}^{n+1}\log(x)\text{d}x\] for \(n\geq1\). Let’s add the above inequalities with \(n=1,2,\cdot\cdot\cdot,N\), we get \[\int_{0}^{1}\log(x)\text{d}x<\log(1)<\int_{1}^{2}\log(x)\text{d}x\]\[+\]\[\int_{1}^{2}\log(x)\text{d}x<\log(2)<\int_{2}^{3}\log(x)\text{d}x\]\[+\]\[\cdot\]\[\cdot\]\[\cdot\]\[+\]\[\int_{N-1}^{N}\log(x)\text{d}x<\log(N)<\int_{N}^{N+1}\log(x)\text{d}x\] thus, \[\int_{0}^{N}\log(x)\text{d}x<\log(1)+\log(2)+\cdot\cdot\cdot+\log(N)<\int_{1}^{N+1}\log(x)\text{d}x\] then, \[\int_{0}^{N}\log(x)\text{d}x<\log(N!)<\int_{1}^{N+1}\log(x)\text{d}x\] The first integral is improper, it is not difficult to show it is convergent, we use the anti-derivative of the function \(x\rightarrow\log(x)\) being \(x\rightarrow x\log x-x\) and knowing that \(\lim_{x \rightarrow 0}x\log x-x=0\) then the integral is convergent. Now let’s continue we get, \[n\log(n)-n<\log(n!)<(n+1)\log(n+1)-n\] Next, let \[d_{n}=\log(n!)-(n+\frac{1}{2})\log(n)+n\] Thus, \[d_{n}-d_{n+1}=\log(n!)-(n+\frac{1}{2})\log(n)+n-\log((n+1)!)+(n+1+\frac{1}{2})\log(n+1)-n-1\]\[=\log(n!)-(n+\frac{1}{2})\log(n)+n-\log(n+1)-\log(n!)+(n+\frac{1}{2})\log(n+1)+\log(n+1)-n-1
\]\[=(n+\frac{1}{2})\log(n+1)-(n+\frac{1}{2})\log(n)-1
\]\[=(n+\frac{1}{2})\log(\frac{n+1}{n})-1
\] With easy algebraic manipulation, we get \[\frac{n+1}{n}=\frac{1+\frac{1}{2n+1}}{1-\frac{1}{2n+1}}
\] The Maclaurin expansion of \(\log(x+1)\) is \[\log(x+1)=x-\frac{x^{2}}{2}+\frac{x^{3}}{3}-\frac{x^{4}}{4}+\frac{x^{5}}{5}+\cdot\cdot\cdot\]
for \(-1<x\leq1\). Now let’s find the Maclaurin expansion of \(\log(1-x)\), to do that we replace \(x\) by \(-x\) in the previous expansion so we get \[\log(1-x)=-x-\frac{x^{2}}{2}-\frac{x^{3}}{3}-\frac{x^{4}}{4}-\frac{x^{5}}{5}-\cdot\cdot\cdot\] for \(-1\leq x<1\). Next let’s substract the second expansion from the first one for \(-1<x<1\), we get \[\log(1+x)-\log(1-x)=x-\frac{x^{2}}{2}+\frac{x^{3}}{3}-\frac{x^{4}}{4}+\frac{x^{5}}{5}+\cdot\cdot\cdot-(-x-\frac{x^{2}}{2}-\frac{x^{3}}{3}-\frac{x^{4}}{4}-\frac{x^{5}}{5}-\cdot\cdot\cdot)\]\[=x-\frac{x^{2}}{2}+\frac{x^{3}}{3}-\frac{x^{4}}{4}+\frac{x^{5}}{5}+\cdot\cdot\cdot+x+\frac{x^{2}}{2}+\frac{x^{3}}{3}+\frac{x^{4}}{4}+\frac{x^{5}}{5}+\cdot\cdot\cdot\]\[=2x+\frac{2}{3}x^{3}+\frac{2}{5}x^{5}+\cdot\cdot\cdot\] thus \[\frac{1}{2}\log(\frac{1+x}{1-x})=x+\frac{1}{3}x^{3}+\frac{1}{5}x^{5}+\cdot\cdot\cdot\] For \(n\geq1\) we have \(0<\frac{1}{2n+1}\leq\frac{1}{3}\) therefore for \(x=\frac{1}{2n+1}\), we get \[\frac{1}{2}\log(\frac{1+\frac{1}{2n+1}}{1-\frac{1}{2n+1}})=\frac{1}{2n+1}+\frac{1}{3}\frac{1}{(2n+1)^{3}}+\frac{1}{5}\frac{1}{(2n+1)^{5}}+\cdot\cdot\cdot\] multiplication by \(2n+1\), we get \[\frac{1}{2}(2n+1)\log(\frac{1+\frac{1}{2n+1}}{1-\frac{1}{2n+1}})=1+\frac{1}{3}\frac{1}{(2n+1)^{2}}+\frac{1}{5}\frac{1}{(2n+1)^{4}}+\cdot\cdot\cdot\] substraction by \(1\) \[\frac{1}{2}(2n+1)\log(\frac{1+\frac{1}{2n+1}}{1-\frac{1}{2n+1}})-1=\frac{1}{3}\frac{1}{(2n+1)^{2}}+\frac{1}{5}\frac{1}{(2n+1)^{4}}+\cdot\cdot\cdot\] therefore \[d_{n}-d_{n+1}=\frac{1}{3}\frac{1}{(2n+1)^{2}}+\frac{1}{5}\frac{1}{(2n+1)^{4}}+\cdot\cdot\cdot\] This implies \[0<d_{n}-d_{n+1}<\frac{1}{3}(\frac{1}{(2n+1)^{2}}+\frac{1}{(2n+1)^{4}}+\cdot\cdot\cdot)\] We recognize a geometric series, therefore we have \[0<d_{n}-d_{n+1}<\frac{1}{3}\frac{1}{(2n+1)^{2}-1}=\frac{1}{12}(\frac{1}{n}-\frac{1}{n+1})\] we get also \[d_{n}-\frac{1}{12n}-(d_{n+1}-\frac{1}{12(n+1)})<0\] From the two previous inequalities we get \[\] \(1.\) The sequence \(\left\{d_{n}\right\}\) is decreasing \[\] \(2.\) The sequence \(\left\{d_{n}-\frac{1}{12n}\right\}\) is increasing \[\] We add that \(\lim_{n \rightarrow \infty}d_{n}-(d_{n}-\frac{1}{12n})=\lim_{n \rightarrow \infty}\frac{1}{12n}=0\), therefore \(\left\{d_{n}\right\}\) and \(\left\{d_{n}-\frac{1}{12n}\right\}\) are adjacent sequences. \[\] This implies that \(\left\{d_{n}\right\}\) converges to a number \(C\) with \[\lim_{n \rightarrow \infty}d_{n}=\lim_{n \rightarrow \infty}d_{n}-\frac{1}{12n}=C\] and that \(C\geq d_{1}-\frac{1}{12}=1-\frac{1}{12}=\frac{11}{12}\). Taking the exponential of \(d_{n}\) we get \[e^{d_{n}}=e^{\log(n!)-(n+\frac{1}{2})\log(n)+n}=\frac{n!}{n^{(n+\frac{1}{2})}e^{-n}}\] therefore \[\lim_{n \rightarrow \infty}\frac{n!}{n^{(n+\frac{1}{2})}e^{-n}}=e^{C}\] The last step is to show that \(e^{C}=\sqrt{2\pi}\). This will be done using Wallis product \[\lim_{n \rightarrow \infty}\frac{2\cdot2\cdot4\cdot4\cdot6\cdot6\cdot\cdot\cdot(2n)(2n)}{1\cdot1\cdot3\cdot3\cdot5\cdot5\cdot\cdot\cdot(2n-1)(2n-1)(2n+1)}=\frac{\pi}{2}\] Rewriting it, we get \[\frac{2\cdot4\cdot6\cdot\cdot\cdot(2n)}{1\cdot3\cdot5\cdot\cdot\cdot(2n-1)\sqrt{2n}}\sim\sqrt{\frac{\pi}{2}}\] we get \[\frac{(2^{n}n!)^{2}}{(2n)!}\frac{1}{\sqrt{2n}}\sim\sqrt{\frac{\pi}{2}}\] Using the approximation \[n!\sim n^{(n+\frac{1}{2})}e^{-n}e^{C}\] we get \[\frac{2^{2n}(n^{2n+1}e^{-2n}e^{2C})}{(2n)^{(2n+\frac{1}{2})}e^{-2n}e^{C}}\frac{1}{\sqrt{2n}}\sim\sqrt{\frac{\pi}{2}}\] Easy algebra gives \[e^{C}\sim\sqrt{2\pi}\] We are dealing with constants, thus \(e^{C}=\sqrt{2\pi}\) \[\] Finally \[\huge n!\sim\sqrt{2\pi n}(\frac{n}{e})^{n}\]
Home -> Solved problems -> Stirling’s formula
Every problem you tackle makes you smarter.
↓ Scroll down for more maths problems↓
↓ ↓
↓ ↓
↓ ↓
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
Home -> Solved problems -> Stirling’s formula