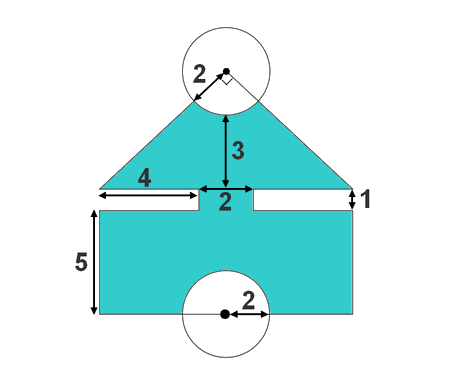
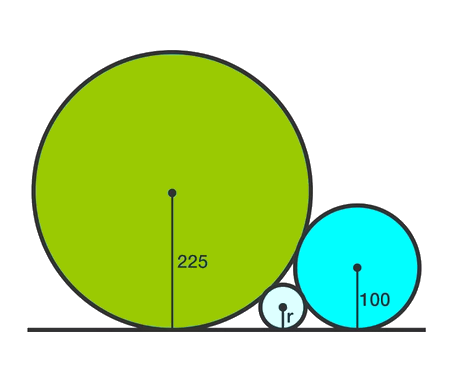
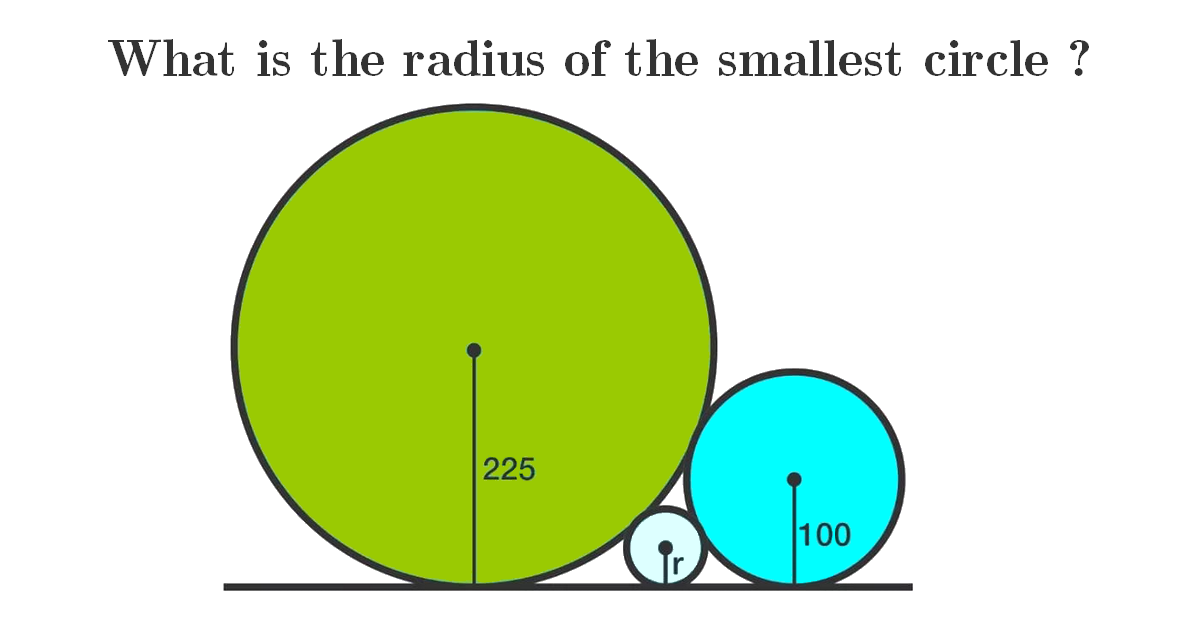
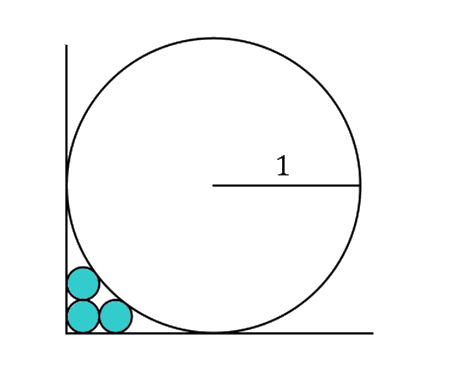What is the radius of the smallest circle ?
Home -> Solved problems -> What is the radius of the smallest circle ?
Solution
To start, we have two circles and a small circle. Let’s calculate the radius \(r\) of the smallest circle. To do that consider the next figure
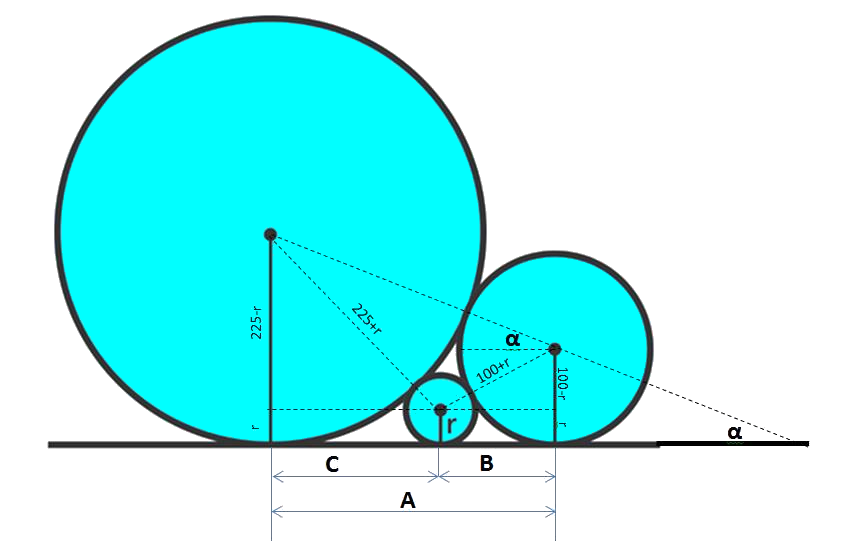
\[\begin{gathered}
\sin \alpha=\frac{225-100}{225+100}=\frac{125}{325} \\\\\Rightarrow \alpha=22,62^{\circ} \\\\ A=(100+225) \cdot \cos \alpha=300 \\\\
A=B+C: \quad B^{2}=(100+r)^{2}-(100-r)^{2}\\\\=\left(100^{2}+200 \mathrm{r}+\mathrm{r}^{2}\right)-\left(100^{2}-200 \mathrm{r}+\mathrm{r}^{2}\right)\\\\=400 r \\\\
C^{2}=(225+r)^{2}-(225-r)^{2}\\\\=\left(225^{2}+450 \mathrm{r}+\mathrm{r}^{2}\right)-\left(225^{2}-450 \mathrm{r}+\mathrm{r}^{2}\right)\\\\=900 r \\\\
A=B+C=20 \sqrt{r}+30 \sqrt{r}\\\\=50 \sqrt{r}=300\\\\ \Rightarrow \sqrt{r}=\frac{300}{50}=6 \\\\\Rightarrow r=36
\end{gathered}\]
Home -> Solved problems -> What is the radius of the smallest circle ?
Every problem you tackle makes you smarter.
↓ Scroll down for more maths problems↓
↓ ↓
↓ ↓
↓ ↓
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
↓ ↓
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?
↓ ↓
↓ ↓
↓ ↓
Home -> Solved problems -> What is the radius of the smallest circle ?