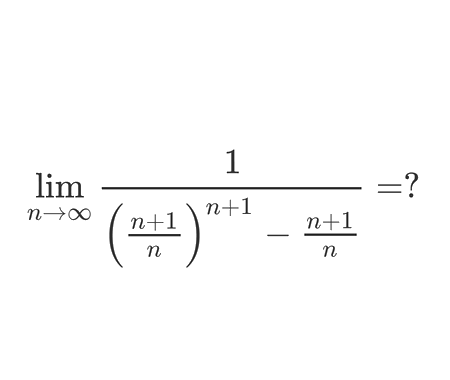Solution : Terme général de la suite – Finding the general term of a sequence

Home -> Solved problems -> Find the general term of the sequence

Solution

In this problem, we aim to find the general term (also called the nth term) of a sequence.
By analyzing the pattern of its first terms, we will identify whether it is an arithmetic sequence, a polynomial sequence, or another type — and derive a formula that gives \(a_n\) in terms of \(n\).
This method provides a powerful way to predict any term in the sequence without listing them all.

To start, we know that we are dealing with a geometric sequence, thus

\[a_{2}=r a_{1}=-\frac{2}{3}\;\;\;\;\;\;\;(1)\]

\(r\) is the common ratio.

An infinite geometric series converges if and only if \(|r|<1\), therefore

\[\begin{aligned} \lim _{n \rightarrow\infty} \sum_{k=1}^{n} a_{k}&=\frac{a_{1}}{1-r} \\\\ \Rightarrow \frac{a_{1}}{1-r}&=\frac{3}{5}\;\;\;\;\;\;\;(2) \end{aligned}\]

\((1)\) and \((2)\), gives

\[\begin{aligned} &\frac{a_{1}}{1+\frac{2}{3 a_{1}}}=\frac{3}{5} \\\\ &\frac{a_{1}}{\frac{3 a_{1}+2}{3 a_{1}}}=\frac{3}{5} \\\\ &\frac{3 a_{1}^{2}}{3 a_{1}+2}=\frac{3}{5} \\\\ &3 a_{1}^{2}=\frac{9}{5} a_{1}+\frac{6}{5} \\\\ &3 a_{1}^{2}-\frac{9}{5} a_{1}-\frac{6}{5}=0 \\\\ &15 a_{1}^{2}-9 a_{1}-6=0 \\\\ &15\left(a_{1}-1\right)\left(a_{1}+\frac{6}{15}\right)=0 \\\\ &a_{1}=1\;\;\;\; or\;\;\;\; a_{1}=-\frac{6}{15} \end{aligned}\]

Let’s discuss the found values

\[\begin{aligned} &a_{1}=1\;\;\;\; gives \;\;\;\;r=-\frac{2}{3}\\\\ &a_{1}=-\frac{6}{15}\;\;\;\; gives \;\;\;\;r=\frac{5}{3}>1\;\;\;\;\text { not possible because }|r|<1\\\\ &\text { So we consider the results } a_{1}=1 \text { and } r=-\frac{2}{3} \end{aligned} \]

The \(n\)-th term of a geometric sequence with first term \(a_{1}\) and common ratio \(r\) is given by

\[\begin{aligned} &a_{n}=a_{1} r^{n-1} \\\\ &a_{n}=\left(-\frac{2}{3}\right)^{n-1} \quad n \geqslant 1 \end{aligned} \]

By identifying the pattern — whether through differences, ratio, or other behaviors — we derived a clean expression for the sequence’s general term \(a_n\).
This formula enables us to compute any term directly, without needing all prior terms.
Understanding how to find the nth term is fundamental in many areas of mathematics, from algebra to series and beyond.

Explore more sequence problems in our Solved Exercises section.

Like & Share the solution on Facebook :

Home -> Solved problems -> Find the general term of the sequence

Every problem you tackle makes you smarter.

↓ Scroll down for more math problems↓

How far apart are the poles ?

Why 0.9999999...=1

Find the volume of the interior of the kiln

Determine the square's side \(x\)

Error to avoid that leads to:

What's the problem ?

Explain your answer without using calculator

Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x} \) has a curvilinear asymptote \(y=x^{2}+2 x+3\)

What values of \(x\) satisfy this inequality

Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?

Only one in 1000 can solve this math problem

Calculate the sum of areas of the three squares

Calculate the following

Find the limit of width and height ratio

Is \(\pi\) an irrational number ?

Solve for \(x \in \mathbb{R}\)

Prove that \(e\) is an irrational number

Prove that

Challenging problem

Solve the equation for \(x \in \mathbb{R}\)

Calculate the following limit

Determine the angle \(x\)

Find the derivative of \(y\) with respect to \(x\)

Solve the equation for real values of \(x\)

Find the equation of the curve formed by a cable suspended between two points at the same height

Calculate the integral

How Tall Is The Table ?

Prove Wallis Product Using Integration

Calculate the radius R

Calculate the volume of Torus using cylindrical shells

Find the derivative of exponential \(x\) from first principles

Find the volume of the square pyramid as a function of \(a\) and \(H\) by slicing method.

Prove that \[\lim_{x \rightarrow 0}\frac{\sin x}{x}=1\]

Prove that

Calculate the half derivative of \(x\)

Find out what is a discriminant of a quadratic equation.

Calculate the rectangle's area

Infinitely nested radicals

Determine the square's side \(x\)

Wonderful math fact: 12542 x 11 = 137962

Calculate the sum

What is the new distance between the two circles ?

Solve the equation for \(x\epsilon\mathbb{R}\)

Calculate the area of the Squid Game diagram blue part

Calculate the limit

Find the infinite sum

Calculate the integral

Prove that

Can we set up this tent ?

Find the value of \(h\)

Is the walk possible?

Find the length of the black segment

Prove that pi is less than 22/7

Find the value of \(x\)

Amazing !

Prove that

What is the weight of all animals ?

Determine the length \(x\) of the blue segment

How many triangles does the figure contain ?

if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?

What is the value of the following infinite product?

Which object weighs the same as the four squares?

What is \((-1)^{\pi}\) equal to?

Can you solve it?

Great Math Problem

Calculate the integral \(\int_{0}^{1}(-1)^{x} d x\)

Find the general term of the sequence

Home -> Solved problems -> Find the general term of the sequence

Solution

Like & Share the solution on Facebook :

Every problem you tackle makes you smarter.

↓ Scroll down for more math problems↓

Share the solution: Find the general term of the sequence