Home -> Solved problems -> Can you solve it? x^2 = 2^x
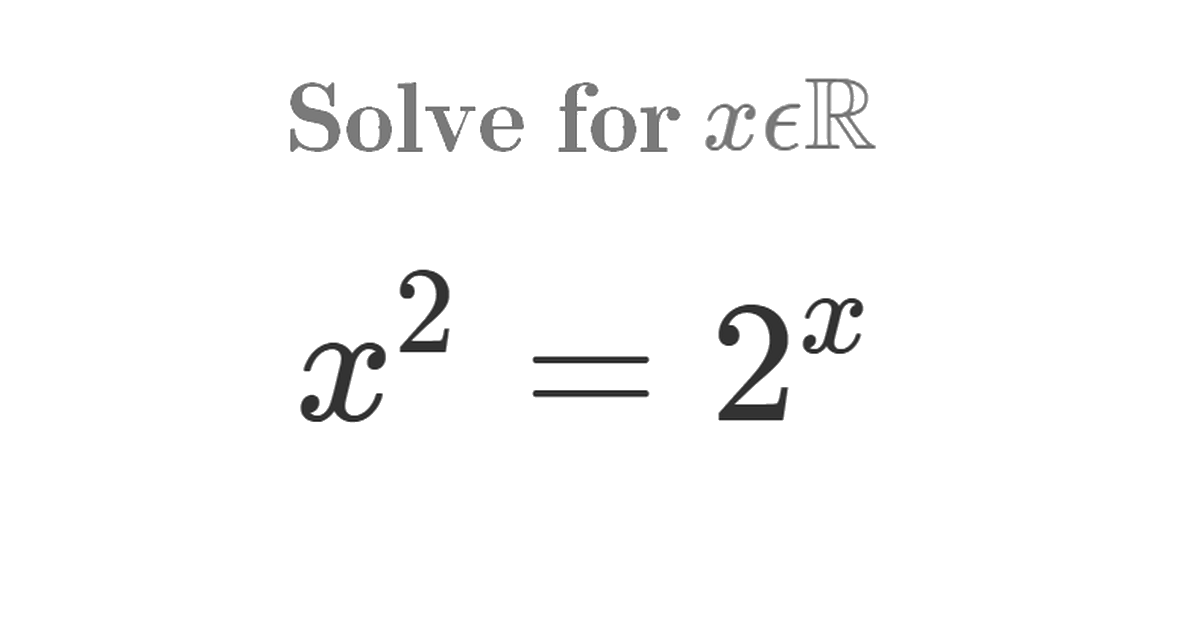
Solution
This visual solution to the equation \(x^2 = 2^x\) explains the real solutions step by step using logarithms and the Lambert W function. Each step is illustrated clearly, so you can follow the reasoning and understand how the equation is solved intuitively. By studying this approach, you’ll gain a deeper understanding of the relationship between exponential and polynomial functions.
To explore more problems like this and see detailed solutions, check out our Solved Exercises page, where visual proofs and step-by-step explanations make learning mathematics engaging and accessible.
\[
\begin{aligned}
x^{2} &= 2^{x} \\
x &\neq 0 \\
\ln(x^{2}) &= \ln(2^{x}) \\
2 \ln|x| &= x \ln 2 \\
x^{-1} \ln|x| &= \frac{1}{2} \ln 2 \\
\text{case (1): } x &> 0 \\
x^{-1} \ln x &= \frac{1}{2} \ln 2 \\
\text{Using Lambert W function:} \\
W(-\ln x \, e^{-\ln x}) &= W(-\ln \sqrt{2}) \\
-\ln x &= W(-\ln \sqrt{2}) \\
x &= e^{-W(-\ln \sqrt{2})}
\end{aligned}
\]
\[
\begin{aligned}
\text{case (2): } x &< 0 \\
(-x)^{-1} \ln(-x) &= -\frac{1}{2} \ln 2 \\
W(-\ln(-x) \, e^{-\ln(-x)}) &= W(\ln \sqrt{2}) \\
-\ln(-x) &= W(\ln \sqrt{2}) \\
x &= -e^{-W(\ln \sqrt{2})}
\end{aligned}
\]
Home -> Solved problems -> Can you solve it? x^2 = 2^x
Every problem you tackle makes you smarter.
↓ Scroll down for more math problems↓
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?
Home -> Solved problems -> Can you solve it? x^2 = 2^x
Enjoy learning mathematics
Mathematics reveals its secrets only to those who approach it with pure love, for its own beauty.
-Archimedes-
The Beauty of Mathematics : It Can Never Lie to You
Mathematics is the queen of the sciences.
Carl Friedrich Gauss
To those who ask what the infinitely small quantity in mathematics is, we answer that it is actually zero. Hence there are not so many mysteries hidden in this concept as they are usually believed to be.
Leonhard Euler
There is geometry in the humming of the strings, there is music in the spacing of the spheres.
Pythagoras
Today’s scientists have substituted mathematics for experiments, and they wander off through equation after equation, and eventually build a structure which has no relation to reality.