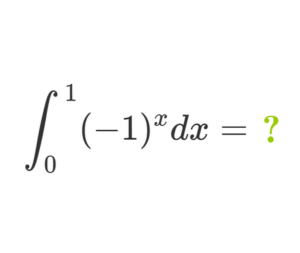Calculate the integral \(\int_{0}^{1}(-1)^{x} d x\)
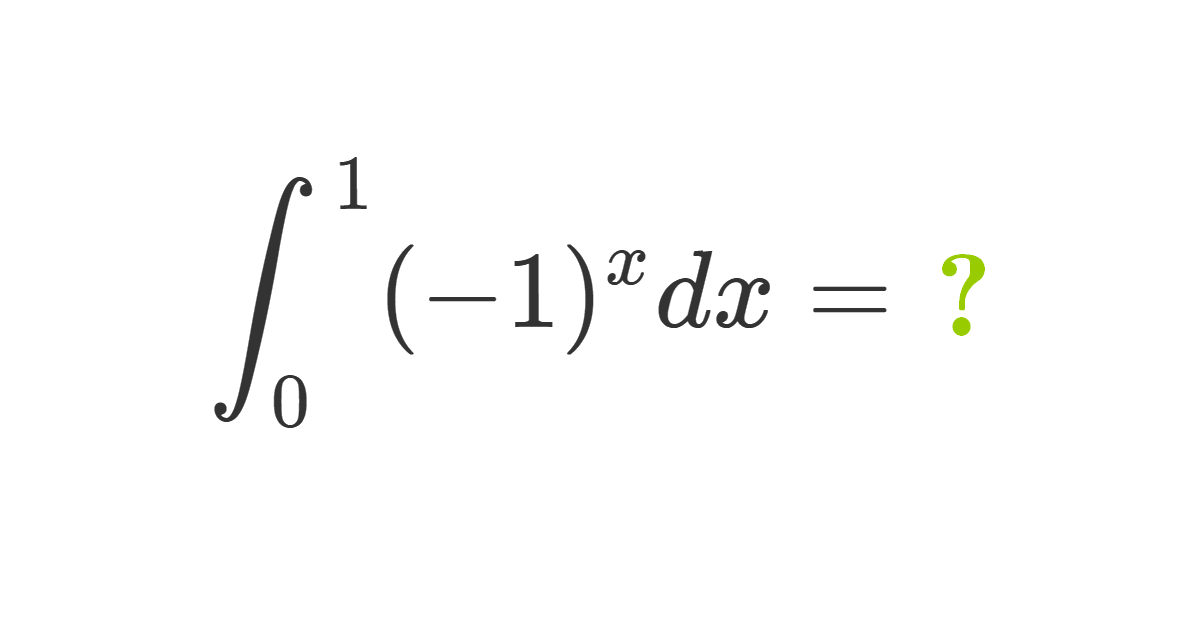
Solution
In this exercise we evaluate the definite integral:
$$
\int_{0}^{1}(-1)^{x}\; dx
$$
At first glance, this looks like a standard integral but reveals surprising structure when we rewrite (-1) as a complex exponential.
In the following solution we will show how recognizing that \( (-1) = e^{\,i\pi} \) leads to a clean integration using the chain rule for exponentials — showing the power of complex analysis techniques even in seemingly simple definite integrals.
This integral illustrates how a real-valued expression \((-1)^{x}\) can be elegantly evaluated by interpreting it as a complex exponential.
The result, expressed in terms of \(i\) and \(\pi\), reinforces the deep connections between real and complex analysis.
Such problems highlight the importance of thinking beyond real functions when tackling integrals, and show how complex exponential representation can simplify unexpected integrals.
Every problem you tackle makes you smarter.
↓ Scroll down for more math problems↓
Share the solution: Calculate the integral \(\int_{0}^{1}(-1)^{x} d x\)