Home -> Solved problems -> Determine the angle x
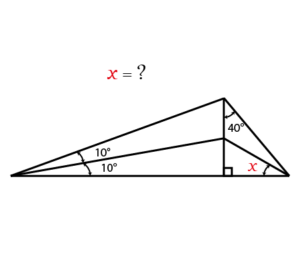
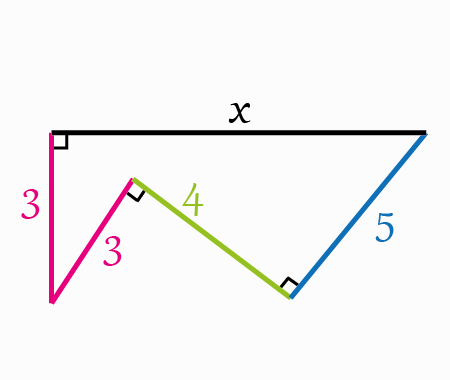
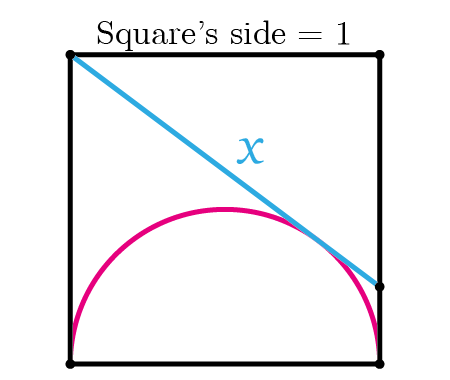
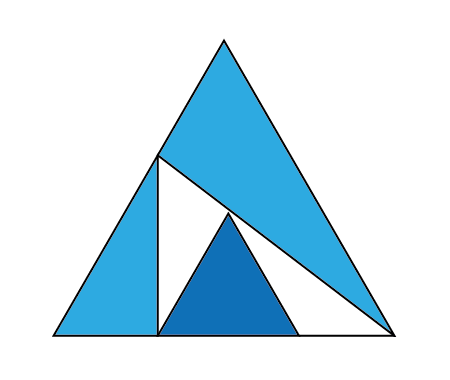
Determine the angle \(x\)
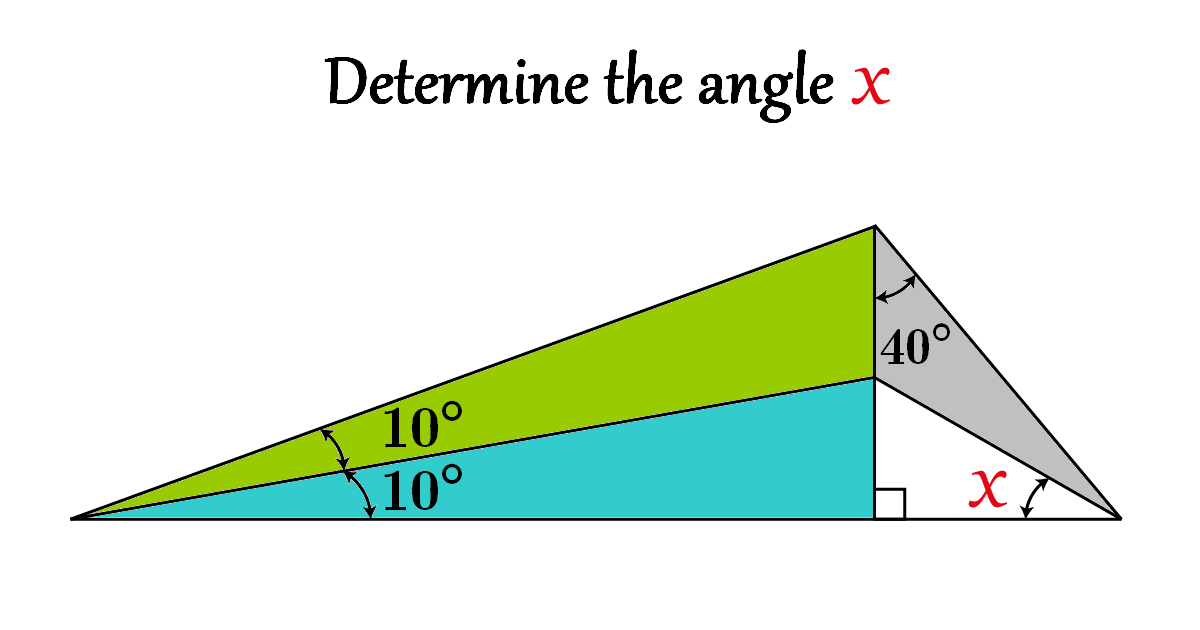
Solution
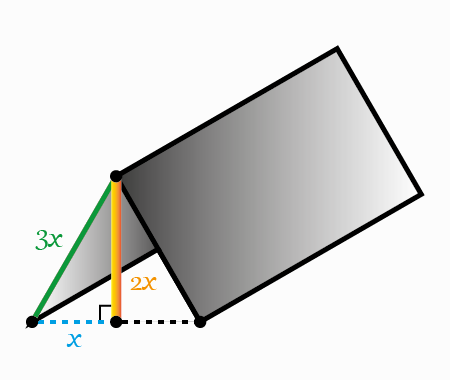
Starting by adding some lengths like it is shown in the next figure
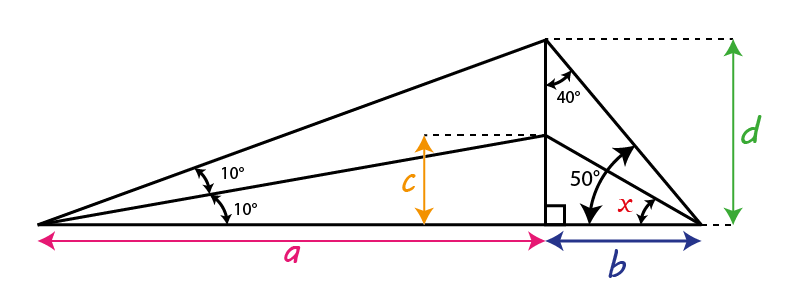
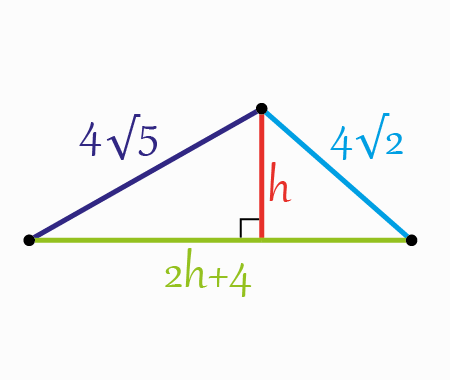
Now, let’s take the triangles in the two next figures
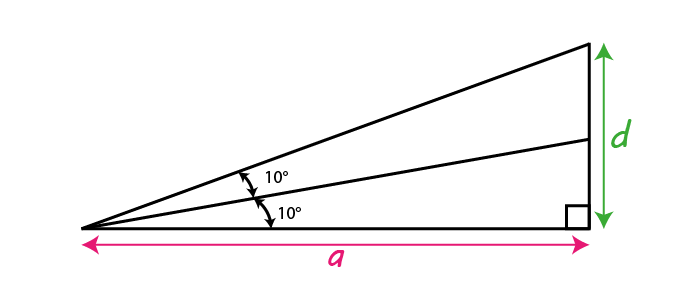
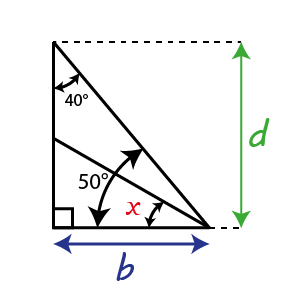
We have \[\tan20°=\frac{d}{a}\] \[and\] \[\tan50°=\frac{d}{b}\] \[\Rightarrow d=b\tan50°=a\tan20°\] \[\Rightarrow\frac{a}{b}=\frac{\tan50°}{\tan20°}\]
For the next triangles
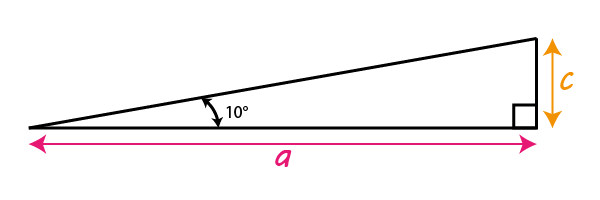
\[\tan10°=\frac{c}{a}\]
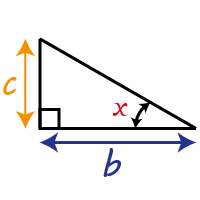
\[\tan x=\frac{c}{b}\]
\[\Rightarrow c=b\tan x=a\tan10°\] \[\Rightarrow\frac{a}{b}=\frac{\tan x}{\tan10°}\]
Using the two results above, we get
\[\frac{\tan x}{\tan10°}=\frac{\tan50°}{\tan20°}\] \[\Rightarrow\tan x=\frac{\tan50°}{\tan20°}\left(\tan10°\right)\]
\[\Rightarrow x=\arctan\left(\frac{\tan50°}{\tan20°}\left(\tan10°\right)\right)=30°\]
Home -> Solved problems -> Determine the angle x
Every problem you tackle makes you smarter.
↓ Scroll down for more math problems↓
if we draw an infinite number of circles packed in a square using the method shown below, will the sum of circles areas approach the square's area?
Home -> Solved problems -> Determine the angle x
Share the solution: Determine the angle x