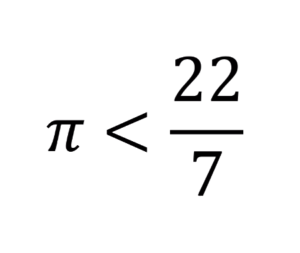Home -> Solved problems -> Prove that pi is less than 22/7
Prove that \(\pi\) is less than \(\frac{22}{7}\)
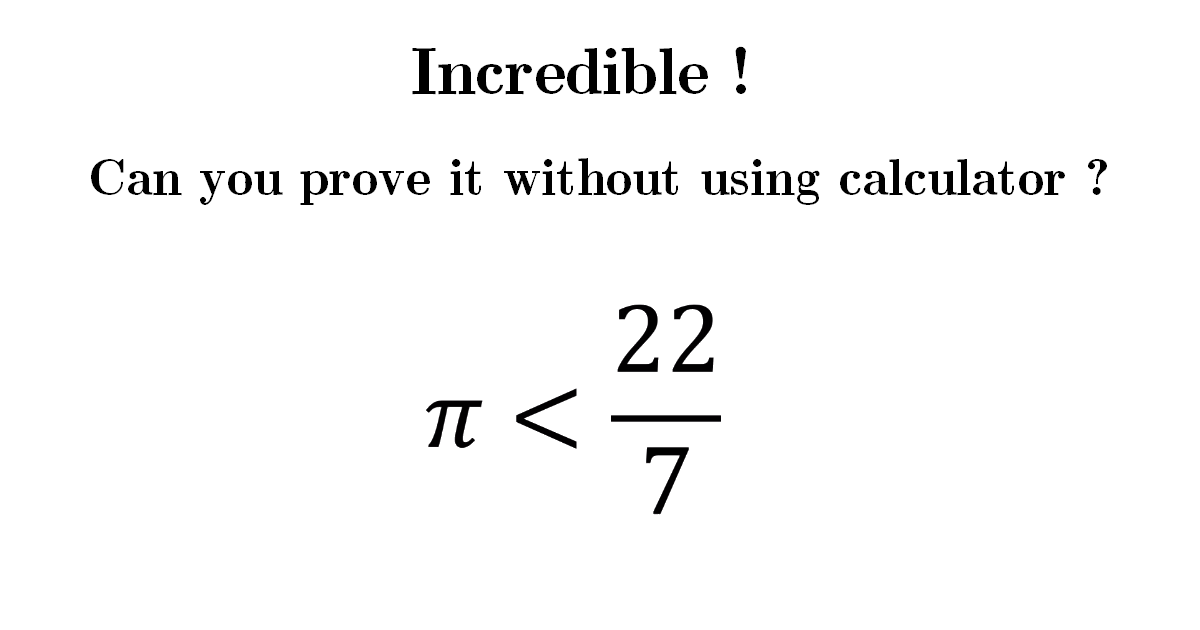
Solution
To prove that \(\pi<\frac{22}{7}\), let’s calculate the next integral
\[\int_{0}^{1} \frac{x^{4}(1-x)^{4}}{1+x^{2}} d x=?\]
The integral is well defined. Next, let’s use the binomial theorem
\[(1-x)^{4}=x^{4}-4 x^{3}+6 x^{2}-4 x+1\]
\[x^{4}(1-x)^{4}=x^{8}-4 x^{7}+6 x^{6}-4 x^{5}+x^{4}\]
Now, let’s use polynomial division, we get
\[\frac{x^{4}(1-x)^{4}}{1+x^{2}}=x^{6}-4 x^{5}+5 x^{4}-4 x^{2}+4-\frac{4}{x^{2}+1}\]
\[\Rightarrow \int_{0}^{1} \frac{x^{4}(1-x)^{4}}{1+x^{2}} d x=\int_{0}^{1}\left(x^{6}-4 x^{5}+5 x^{4}-4 x^{2}+4-\frac{4}{x^{2}+1}\right) d x\]
\[=\frac{x^{7}}{7}-\frac{4 x^{6}}{6}+x^{5}-\frac{4 x^{3}}{3}+4 x-\left.4 \arctan (x)\right|_{0} ^{1}\]
\[=\frac{1}{7}-\frac{4}{6}+1-\frac{4}{3}+4-4\left(\frac{\pi}{4}\right)-(0-0+0-0+0-4(0))\]
\[=\frac{22}{7}-\pi\]
\[\frac{x^{4}(1-x)^{4}}{1+x^{2}}>0 \quad \forall x \in(0,1)\]
\[\Rightarrow \int_{0}^{1} \frac{x^{4}(1-x)^{4}}{1+x^{2}}>0\]
\[\Rightarrow \frac{22}{7}-\pi>0\]
\[\huge \Rightarrow \pi<\frac{22}{7}\]
Home -> Solved problems -> Prove that pi is less than 22/7
Recommended for you :
Home -> Solved problems -> Prove that pi is less than 22/7
Share the solution: Prove that pi is less than 22/7