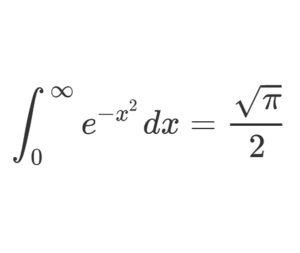Home -> Solved problems -> The Gaussian integral
The Gaussian integral
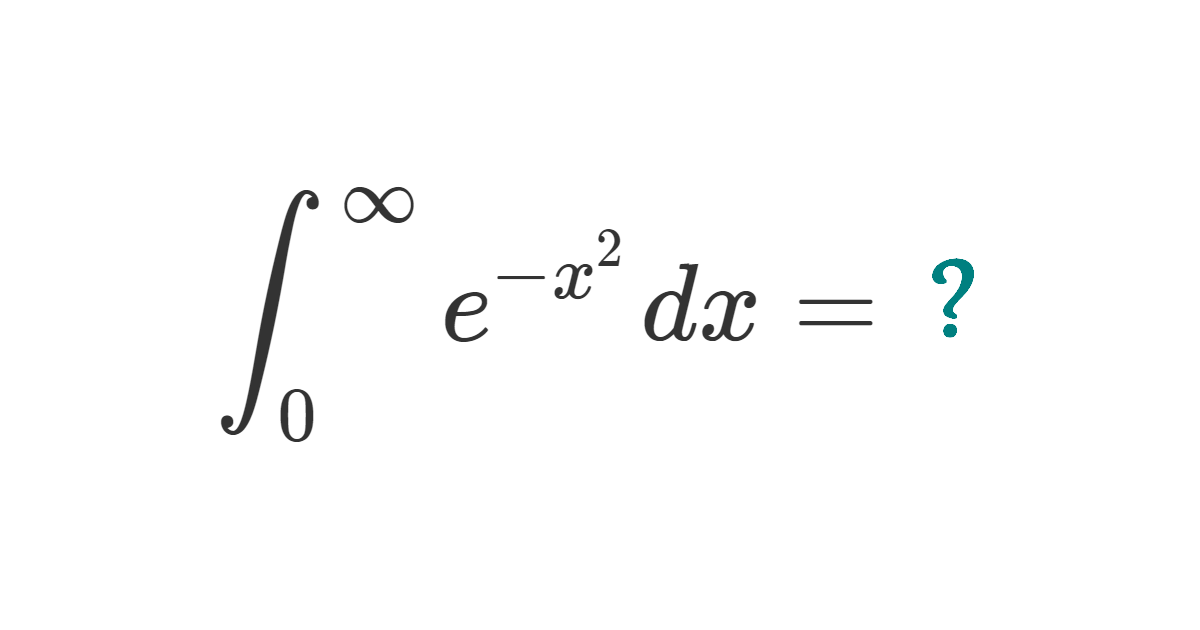
Solution
Consider the double integrals: \(\int_{0}^{\infty} \int_{0}^{\infty} e^{-\left(x^{2}+y^{2}\right)} d x d y\).
Looking at the limits of integration, we see that the first integration is along a vertical strip extending from \(y=0\) to \(y=\infty\). The second integration is along an horizontal strip from \(x=0\) to \(x=\infty\). The next figure shows the region of integration
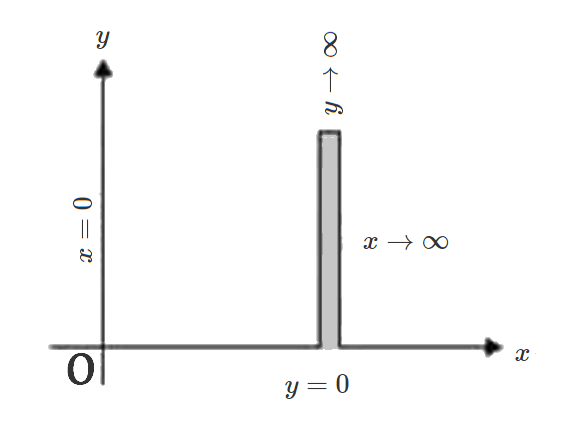
By changing to polar co-ordinates, this region can be covered by radial strips going from \(r=0\) to \(r=\infty\). The strip begins from \(\theta=0\) and goes upto \(\theta=\frac{\pi}{2}\)
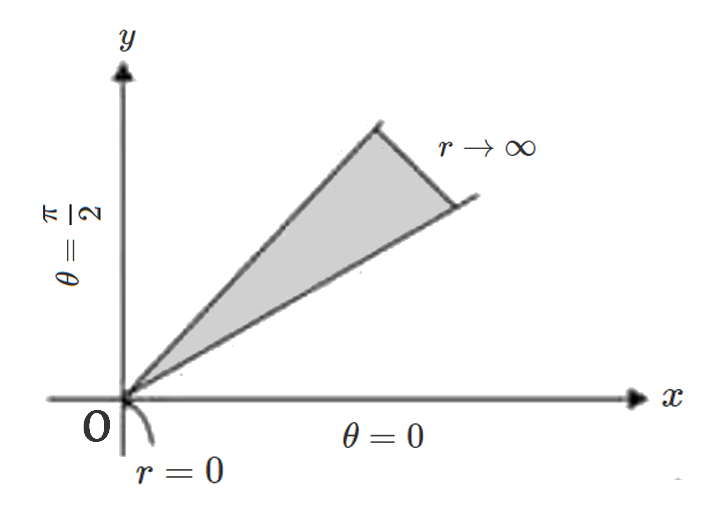
Therefore, \[\begin{aligned}
\int_{0}^{\infty} \int_{0}^{\infty} e^{-\left(x^{2}+y^{2}\right)} d x d y &=\int_{0}^{ \frac{\pi}{2}} \int_{0}^{\infty} e^{-r^{2}} r d r d \theta \\\\
&=-\frac{1}{2} \int_{0}^{\frac{\pi}{2}} \int_{0}^{\infty}(-2 r) e^{-r^{2}} d r d \theta\\\\&=-\frac{1}{2} \int_{0}^{\frac{\pi}{2}}\left[e^{-r^{2}}\right]_{0}^{\infty} d \theta \\\\
&=-\frac{1}{2} \int_{0}^{\frac{\pi}{2}}(0-1) d \theta\\\\&=\frac{1}{2} \int_{0}^{\frac{\pi}{2}} 1 d \theta\\\\&=\frac{\pi}{4}
\end{aligned}\]
Let, \(I=\int_{0}^{\infty} e^{-x^{2}} d x \;\;\;\;\;\;\; (1)\)
Also, \(I=\int_{0}^{\infty} e^{-y^{2}} d y \;\;\;\;\;\;\; (2)\)
By multiplying \((1)\) and \((2)\), \[\begin{aligned}
&I^{2}=\int_{0}^{\infty} \int_{0}^{\infty} e^{-\left(x^{2}+y^{2}\right)} d x d y=\frac{\pi}{4} \\\\
&I=\sqrt{\frac{\pi}{4}}=\frac{\sqrt{\pi}}{2}
\end{aligned}\]
\[\large \Rightarrow\int_{0}^{\infty} e^{-x^{2}} d x=\frac{\sqrt{\pi}}{2}\]
Home -> Solved problems -> The Gaussian integral
Related Topics: Solved Problems
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
Home -> Solved problems -> The Gaussian integral
Share the solution: The Gaussian integral