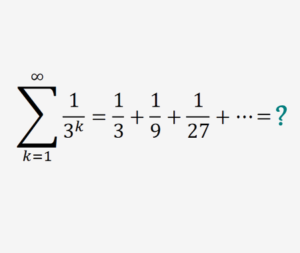Home -> Solved problems -> Find the infinite sum (1/3)^k
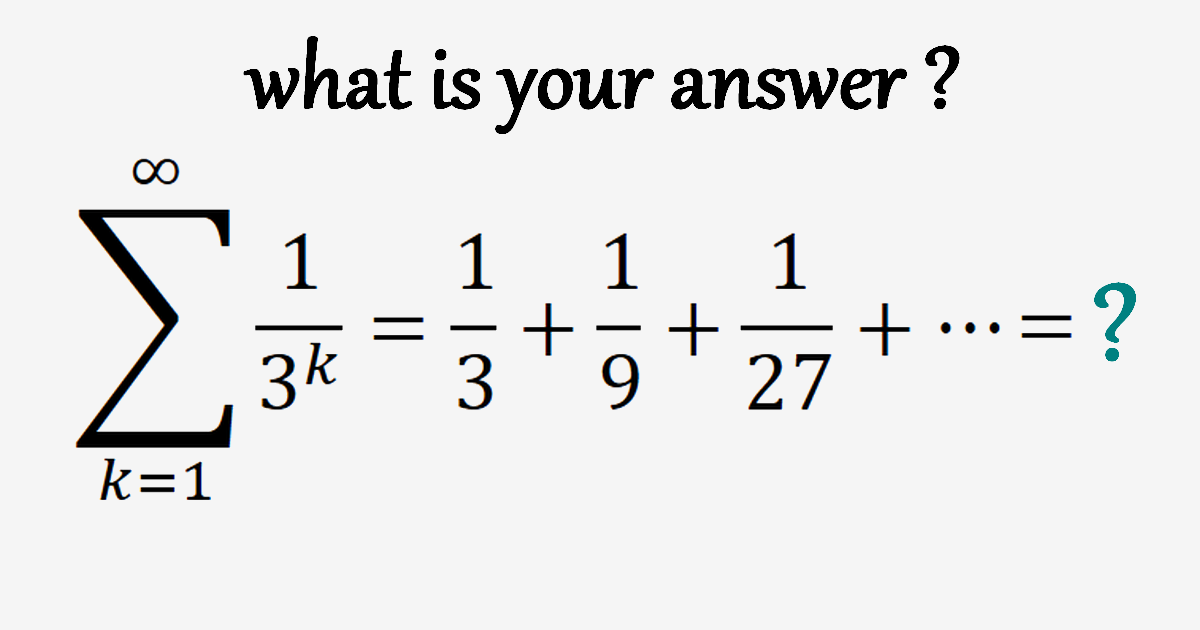
Solution
First, let’s show that the series converges: \[|\frac{1}{3}|=\frac{1}{3}<1\] Thus, the series is convergent.
\[\begin{aligned}
&S=\sum_{k=1}^{\infty} \frac{1}{3^{k}}=\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\cdots \\\\\\
&3 S=1+\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\cdots \\\\\\
&3 S-S=1 \\\\\\
&S=\frac{1}{2}
\end{aligned}\]
Home -> Solved problems -> Find the infinite sum (1/3)^k
Related Topics: Solved Problems
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
Home -> Solved problems -> Find the infinite sum (1/3)^k
Share the solution: Find the infinite sum (1/3)^k