Home -> Solved problems -> Find the value of h
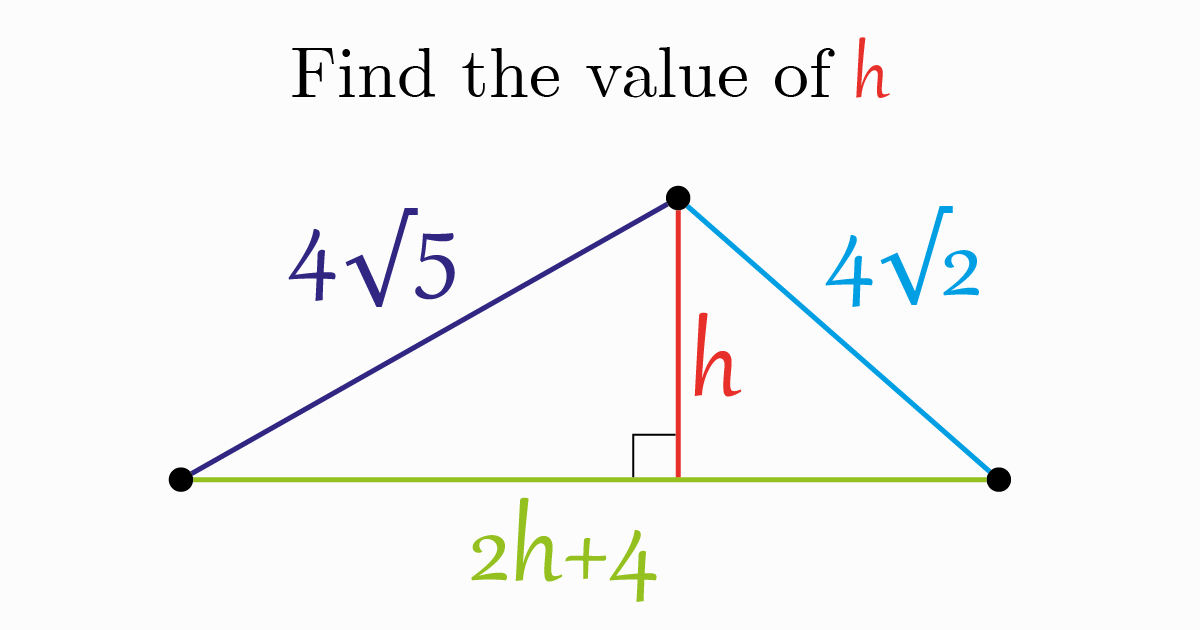
Solution
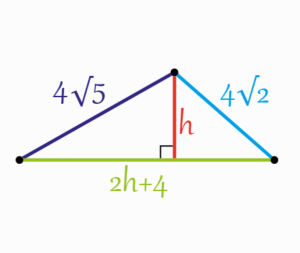
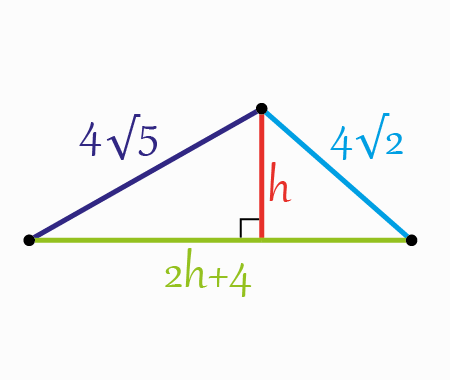
To start, let’s add some sections like it is shown in the next figure
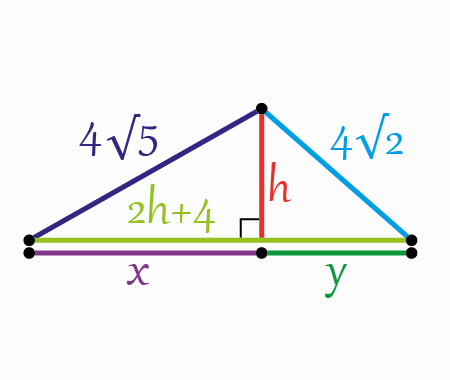
Using Pythagoras theorem within the two next triangles
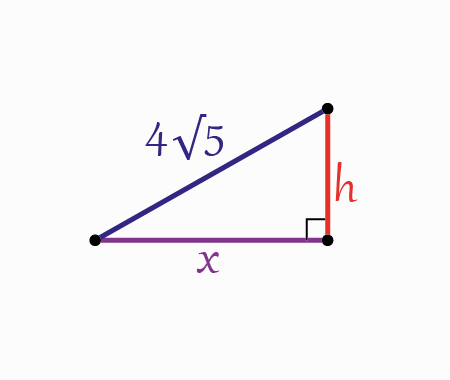
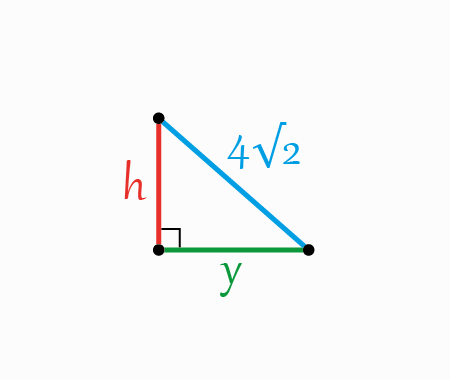
We get, \[\begin{aligned}
&(4 \sqrt{5})^{2}=h^{2}+x^{2}\;\;\;\;\;\;\;(1) \\\\
&(4 \sqrt{2})^{2}=h^{2}+y^{2}\;\;\;\;\;\;\;(2)
\end{aligned}\]
Using \((1) – (2)\), we get \[\begin{aligned}
x^{2}-y^{2} &=(4 \sqrt{5})^{2}-(4 \sqrt{2})^{2} \\\\
&=80-32 \\\\
&=48 \\\\
(x-y)(x+y) &=48 \\\\
x-y &=\frac{48}{x+y} \\\\
\Rightarrow x-y &=\frac{48}{2 h+4}\;\;\;\;\;\;\;(3) \\\\
x+y&= 2 h+4\;\;\;\;\;\;\;\;(4)
\end{aligned}\] Adding \((3) + (4)\), we get \[\begin{aligned}
2 x&=2 h+4+\frac{48}{2 h+4} \\\\
x&=h+2+\frac{24}{2 h+4}\;\;\;\;\;\;\;(5)
\end{aligned}\] Using \((1)\) and \((5)\), we get \[(4 \sqrt{5})^{2}=h^{2}+\left(h+2+\frac{24}{2 h+4}\right)^{2}\] After expanding the previous expression, we get the equation \[h^{4}+6 h^{3}-14 h^{2}-96 h-32=0\] By a simple verification, we can show that \(-4\) and \(4\) are two roots of the equation and now let’s try to find the other roots \[\begin{aligned}
h^{4}+6 h^{3}-14 h^{2}-96 h-32 &=(h-4)(h+4)\left(a h^{2}+b h+c\right) \\\\
&=\left(h^{2}-16\right)\left(a h^{2}+b h+c\right) \\\\
&=a h^{4}+b h^{3}+(c-16 a) h^{2}-16 b h-16 c
\end{aligned}\] Therefore, \[\begin{aligned}
&a=1 \\
&b=6 \\
&c=2
\end{aligned}\]
Now, we are dealing with the equation \[(h-4)(h+4)\left(h^{2}+6 h+2\right)=0\] Let’s solve the quadratic equation \[\begin{aligned}
&h^{2}+6 h+2=0 \\\\
\Delta &=6^{2}-4 \cdot 2 \\\\
&=36-8 \\\\
&=28 \Rightarrow \sqrt{\Delta}=\sqrt{28}=2 \sqrt{7} \\\\
\Longrightarrow h &=-3-\sqrt{7} \\\\
& or \\\\
h &=-3+\sqrt{7}
\end{aligned}\] \[\Rightarrow h \in\{-3- \sqrt{7},-4,-3+\sqrt{7}, 4\}\] We have only one positive root which is \[\huge h=4\]
Home -> Solved problems -> Find the value of h
Related Topics: Solved Problems
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
Home -> Solved problems -> Find the value of h
Share the solution: Find the value of h