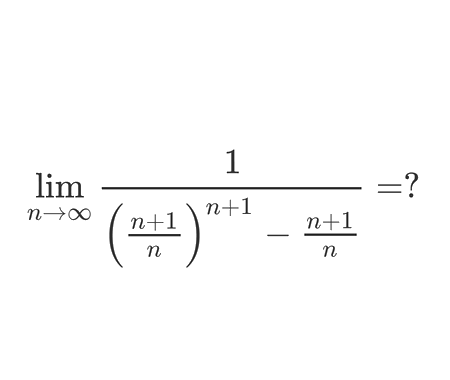Home -> Solved problems -> Calculate the limit
Find: \(\lim_{n \rightarrow \infty}\frac{1}{\left(\frac{n+1}{n}\right)^{n+1}-\frac{n+1}{n}}\)
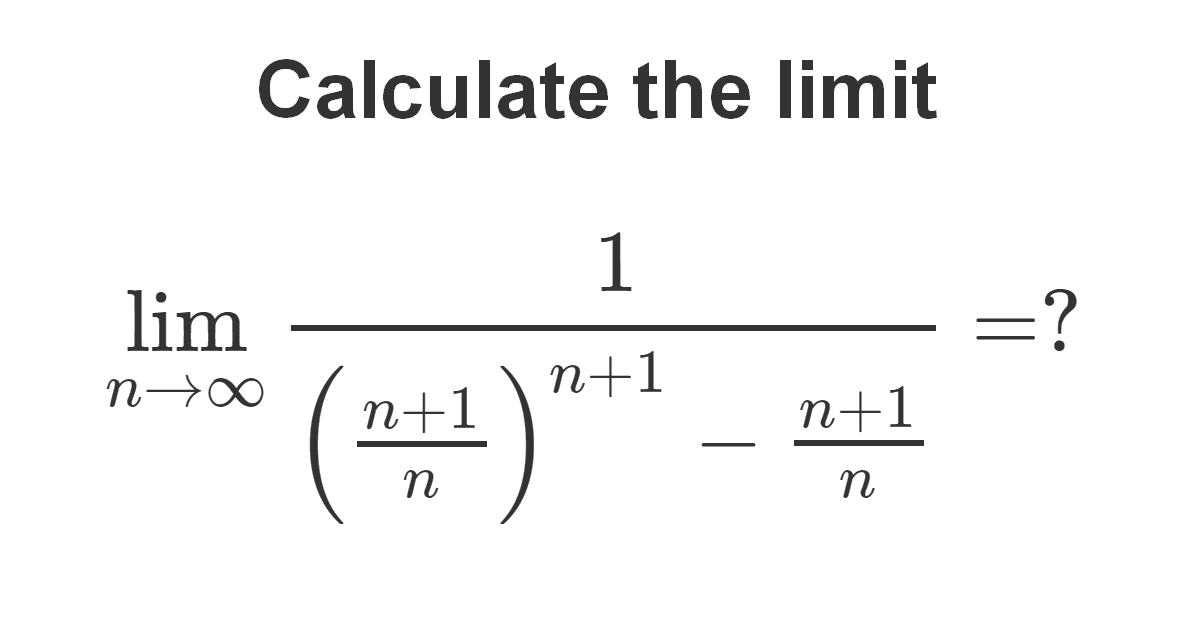
Solution
\[\begin{aligned}
\lim_{n \rightarrow \infty}\frac{1}{\left(\frac{n+1}{n}\right)^{n+1}-\frac{n+1}{n}}=&\lim_{n \rightarrow \infty}\left[\left(\frac{n+1}{n}\right)^{n+1}-\frac{n+1}{n}\right]^{-1}\\\\
=&\lim_{n \rightarrow \infty}\left[\left(1+\frac{1}{n}\right)^{n+1}-\left(1+\frac{1}{n}\right)\right]^{-1}\\\\
=&\lim_{n \rightarrow \infty}\left[\left(1+\frac{1}{n}\right)^{n} \left(1+\frac{1}{n}\right)-\left(1+\frac{1}{n}\right)\right]^{-1}\\\\
=&\frac{1}{e-1}
\end{aligned}\]
Home -> Solved problems -> Calculate the limit
Related Topics
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
Home -> Solved problems -> Calculate the limit
Share the solution: Calculate the limit