Home -> Solved problems -> A point P lies inside a square ABCD
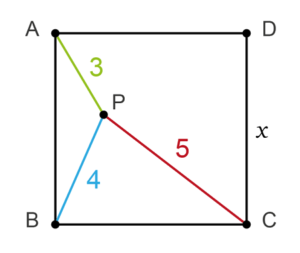
A point P lies inside a square ABCD
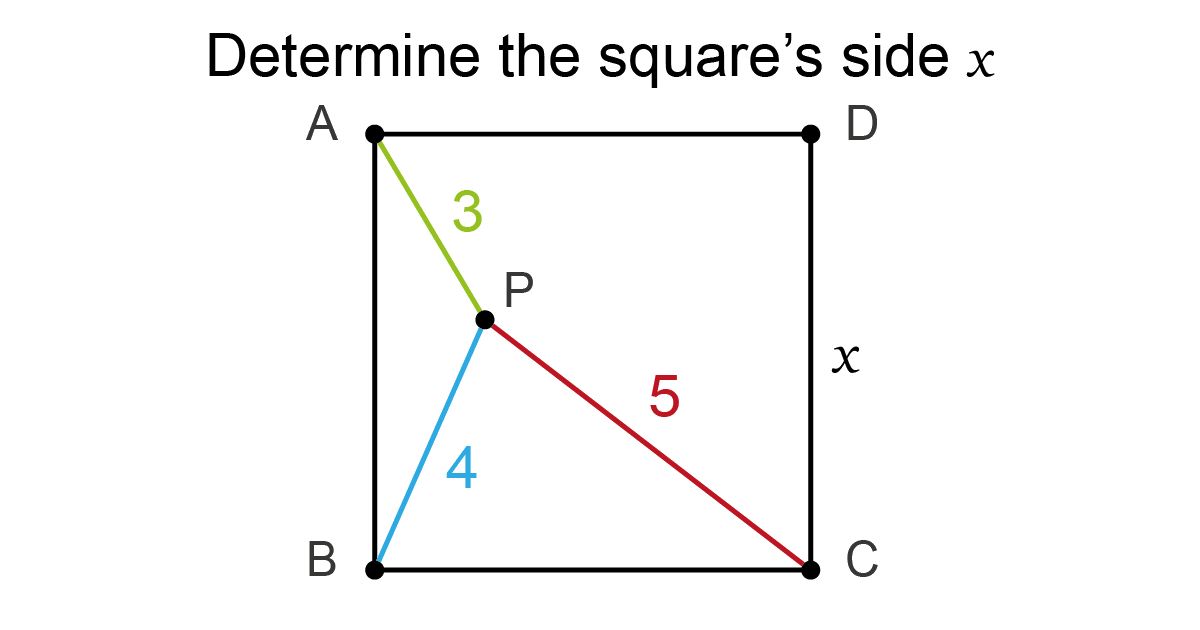
Solution
To start, let’s add an angle \(\alpha\) like it is shown in the next figure
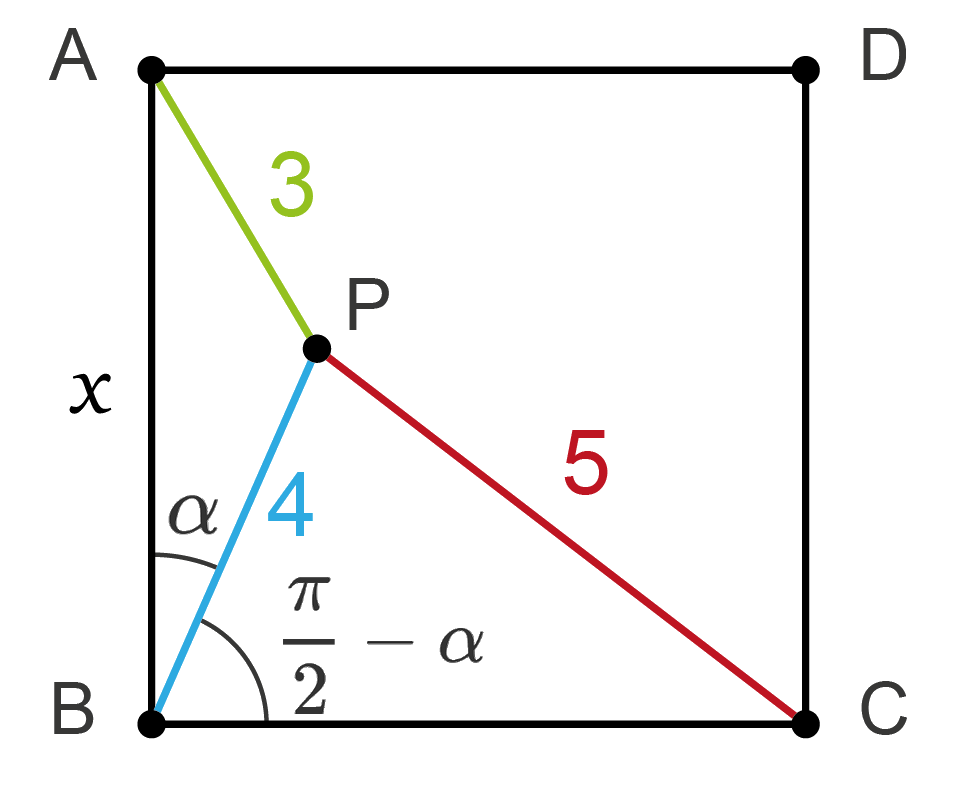
Applying the law of cosines in the triangle \(\triangle BPA\), we get
\[\begin{aligned}
A P^{2} &=AB^{2}+BP^{2}-2AB\cdot BP \cos\alpha \\\\
3^{2} &=x^{2}+4^{2}-8 x \cos \alpha \\\\
9 &=x^{2}+16-8 x \cos \alpha \\\\
\cos \alpha &=\frac{x^{2}+7}{8 x}
\end{aligned}\]
Applying the law of cosines in the triangle \(\triangle BPC\), we get
\[\begin{aligned}
PC^{2} &=BP^{2}+BC^{2}-2BP\cdot BC \cos \left(\frac{\pi}{2}-\alpha\right) \\\\
5^{2} &=4^{2}+x^{2}-8 x \cos \left(\frac{\pi}{2}-\alpha\right) \\\\
& \cos \left(\frac{\pi}{2}-\alpha\right)=\sin \alpha \\\\
\Rightarrow 25 &=16+x^{2}-8 x \sin \alpha \\\\
\sin \alpha &=\frac{x^{2}-9}{8 x}
\end{aligned}\]
We know that \(\cos^{2}\alpha+\sin^{2}\alpha=1\), thus
\[\Rightarrow\left(\frac{x^{2}+7}{8 x}\right)^{2}+\left(\frac{x^{2}-9}{8 x}\right)^{2}=1\] \[\begin{aligned}
\frac{x^{4}+14 x^{2}+49}{64 x^{2}}+\frac{x^{4}-18 x^{2}+81}{64 x^{2}} &=1 \\\\
2 x^{4}-4 x^{2}+130 &=64 x^{2} \\\\
2 x^{4}-68 x^{2}+130 &=0 \\\\
x^{4}-34 x^{2}+65 &=0
\end{aligned}\]
Let,
\[\begin{aligned}
y=x^{2} \\\\
\Rightarrow y^{2}-34 y+65=0\\\\
y \in\{17-4 \sqrt{14}, \;4 \sqrt{14}+17\}
\end{aligned}\]
\[\Rightarrow x \in\{-\sqrt{17-4 \sqrt{14}}, \sqrt{17-4 \sqrt{14}},-\sqrt{4 \sqrt{14}+17}, \sqrt{4 \sqrt{14}+17}\}
\]
We can eliminate \(x =-\sqrt{17-4 \sqrt{14}}\) and \(x =-\sqrt{4 \sqrt{14}+17}\) because \(x>0\)
We can also eliminate \(x =\sqrt{17-4 \sqrt{14}}\) because \(x\) must be larger than \(5\) so \(P\) is contained inside the square.
So the only possible solution is \[\large x=\sqrt{4 \sqrt{14}+17}
\]
Home -> Solved problems -> A point P lies inside a square ABCD
Related Topics
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}
\) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
Home -> Solved problems -> A point P lies inside a square ABCD
Share the solution: A point P lies inside a square ABCD