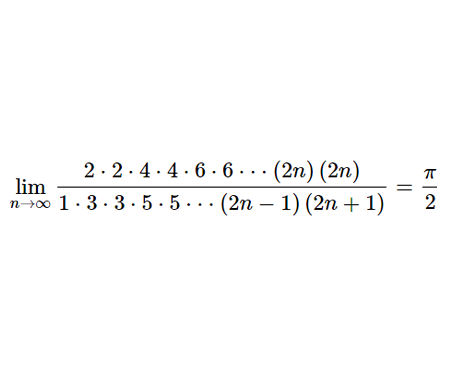Home -> Solved problems -> 98 disappear

Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?

Solution

We have \[\frac{1}{99 \cdot 99}=\frac{1}{9801}\] \[=0.000102030405 \ldots 9596979900010203 \ldots\] Now, let’s find the MacLaurin / Taylor Series for \(f(x)=\frac{1}{1-x}\)
\[\frac{1}{1-x}=1+x+x^{2}+x^{3}+x^{4}+\cdots\;\;\;\;\;\;\;|x|<1\] \[\Rightarrow\frac{1}{(1-x)(1-x)}=1+2 x+3 x^{2}+4 x^{3}+5 x^{4}+\cdots\;\;\;\;\;\;\;|x|<1\]
Let \(x=10^{-2}\), we can explain the pattern expanded from \(\frac{1}{9801}\). the reason for disappearance of the number \(98\) is caused by the propagation of the carry \(1\) from \(100x^{99}\). Similar patterns can be deduced by putting \(x=10^{-1}, 10^{-3}, 10^{-4}, 10^{-5}, \ldots\) to get \[\frac{1}{9 \cdot 9}, \frac{1}{999 \cdot 999}, \frac{1}{9999 \cdot 9999}, \frac{1}{99999 \cdot 99999}, \ldots\]
Home -> Solved problems -> 98 disappear

Related Topics

Find the volume of the square pyramid as a function of \(a\) and \(H\) by slicing method.
Solution
Prove that \[\lim_{x \rightarrow 0}\frac{\sin x}{x}=1\]
Solution
Prove that
Solution
Calculate the half derivative of \(x\)
Solution
Prove Wallis Product Using Integration
Solution
Calculate the radius R
Solution
Calculate the volume of Torus using cylindrical shells
Solution
Find the derivative of exponential \(x\) from first principles
Solution
Calculate the sum of areas of the three squares
Solution
Find the equation of the curve formed by a cable suspended between two points at the same height
Solution
Solve the equation for real values of \(x\)
Solution
Solve the equation for \(x\epsilon\mathbb{R}\)
Solution
Determine the angle \(x\)
Solution
Calculate the following limit
Solution
Calculate the following limit
Solution
Calculate the integral
Solution
Challenging problem
Solution
Prove that
Solution
Prove that \(e\) is an irrational number
Solution
Find the derivative of \(y\) with respect to \(x\)
Solution
Find the limit of width and height ratio
Solution
How Tall Is The Table ?
Solution
Why 0.9999999...=1
Solution
Solve the equation for \(x \in \mathbb{R}\)
Solution
Calculate the following
Solution
Is \(\pi\) an irrational number ?
Solution
How far apart are the poles ?
Solution
Solve for \(x \in \mathbb{R}\)
Solution
What values of \(x\) satisfy this inequality
Solution
Prove that the function \(f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x} \) has a curvilinear asymptote \(y=x^{2}+2 x+3\)
Solution
Why does the number \(98\) disappear when writing the decimal expansion of \(\frac{1}{9801}\) ?
Solution
Home -> Solved problems -> 98 disappear

Share the solution: 98 disappear