Home -> Solved problems -> Curvilinear asymptote
Find out how to find the equation of a rational function curvilinear asymptote
Solution
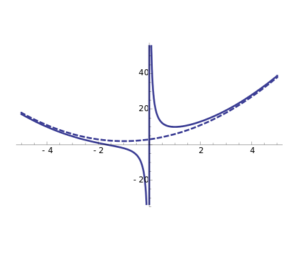
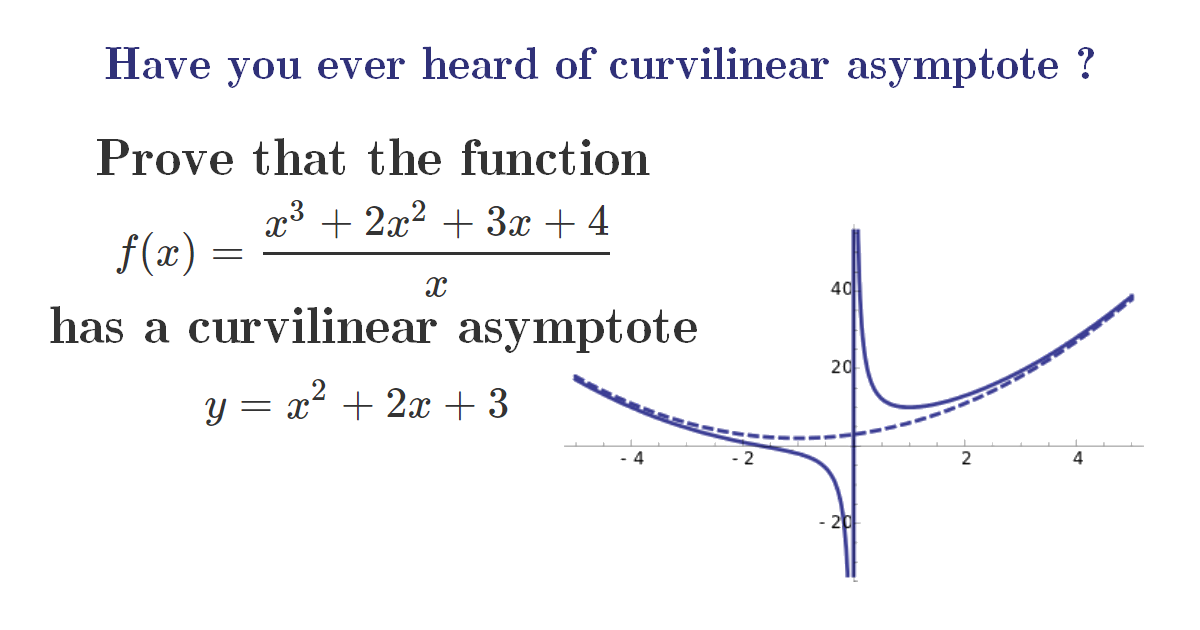
\(f\) is a function defined on \(]-\infty, 0[\cup] 0, \infty[\) by: \[f(x)=\frac{x^{3}+2 x^{2}+3 x+4}{x}\] We are interested in studying \(f\) as \(x\) approaches infinity (\(-\infty\) and \(\infty\))
\[\begin{aligned}
\lim _{x \rightarrow\infty} f(x) &=\lim _{x \rightarrow\infty} \frac{x^{3}+2 x^{2}+3 x+4}{x} \\\\
&=\lim _{x \rightarrow\infty} \frac{x^{3}\left(1+\frac{2}{x}+\frac{3}{x^{2}}+\frac{4}{x^{3}}\right)}{x} \\\\
&=\lim _{x \rightarrow\infty} x^{2}\left(1+\frac{2}{x}+\frac{3}{x^{2}}+\frac{4}{x^{3}}\right) \\\\
&=\lim _{x \rightarrow\infty} x^{2}=\infty
\end{aligned}\] Now, let’s study the behavior of \(f\) relative to \(x\) as \(x\) approaches \(\infty\) \[\begin{aligned}
\lim _{x \rightarrow\infty} \frac{f(x)}{x} &=\lim _{x \rightarrow\infty} \frac{x^{3}+2 x^{2}+3 x+4}{x^{2}} \\\\
&=\lim _{x \rightarrow\infty} x\left(1+\frac{2}{x}+\frac{3}{x^{2}}+\frac{4}{x^{3}}\right) \\\\
&=\lim _{x \rightarrow\infty} x=\infty
\end{aligned}\] Therefore, \(f\) has no slant asymptote when \(x\) approaches \(\infty\).
Thus, we increase the degree of power of \(x\) and we study the behavior of the function \(f\) relative to \(x^{2}\) as \(x\) approaches \(\infty\) \[\begin{aligned}
\lim _{x \rightarrow \infty} \frac{f(x)}{x^{2}} &=\lim _{x \rightarrow \infty} \frac{x^{3}+2 x^{2}+3 x+4}{x^{3}} \\\\
&=\lim _{x \rightarrow\infty} 1+\frac{2}{x}+\frac{3}{x^{2}}+\frac{4}{x^{3}} \\\\
&=1
\end{aligned}\] At this step, we know that we are dealing with a parabola with equation of general form: \(y=ax^{2}+bx+c\), knowing that we have already find \(a=1\) the equation becomes: \(y=x^{2}+bx+c\). Now, let’s try to find \(b\) and \(c\) \[\begin{aligned}
\lim _{x \rightarrow+\infty} \frac{f(x)-x^{2}}{x} &=\lim _{x \rightarrow \infty} \frac{\frac{x^{3}+2 x^{2}+3 x+4}{x}-x^{2}}{x} \\\\
&=\lim _{x \rightarrow \infty} \frac{x^{3}+2 x^{2}+3 x+4-x^{3}}{x^{2}} \\\\
&=\lim _{x \rightarrow \infty} \frac{2 x^{2}+3 x+4}{x^{2}} \\\\
&=\lim _{x \rightarrow \infty} \frac{x^{2}\left(2+\frac{3}{x}+\frac{4}{x^{2}}\right)}{x^{2}} \\\\
&=\lim _{x \rightarrow \infty} 2+\frac{3}{x}+\frac{4}{x^{2}} \\\\
&=2
\end{aligned}\] \[\Rightarrow b=2\] Therefore, \[y=x^{2}+2x+c\] Now, let’s try to find \(c\) \[\begin{aligned}
\lim _{x \rightarrow \infty} f(x)-x^{2}-2 x &=\lim _{x \rightarrow \infty} \frac{x^{3}+2 x^{2}+3 x+4}{x}-x^{2}-2 x \\\\
&=\lim _{x \rightarrow \infty} \frac{x^{3}+2 x^{2}+3 x+4-x\left(x^{2}+2 x\right)}{x} \\\\
&=\lim _{x \rightarrow \infty} \frac{x^{3}+2 x^{2}+3 x+4-x^{3}-2 x^{2}}{x} \\\\
&=\lim _{x \rightarrow \infty} \frac{3 x+4}{x} \\\\
&=\lim _{x \rightarrow \infty} \frac{x\left(3+\frac{4}{x}\right)}{x} \\\\
&=\lim _{x \rightarrow \infty} 3+\frac{4}{x}=3=c
\end{aligned}\] For \(-\infty\) we use the same steps as \(\infty\) and we will find out that the parabola: \(y=x^{2}+2 x+3\) is also a parabolic asymptote for the function \(f\) but as \(x\) approaches \(-\infty\). \[\] Let’s recap, \(f\) has a curvilinear asymptote as \(x\) approaches \(-\infty\) and \(\infty\) which is a parabolic asymptote \[\huge y=x^{2}+2 x+3\]
Home -> Solved problems -> Curvilinear asymptote
Related Topics
Home -> Solved problems -> Curvilinear asymptote
Share the solution: Curvilinear asymptote