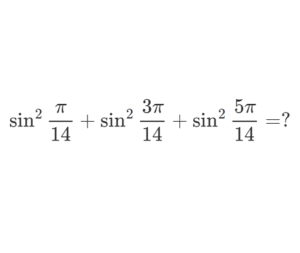Home -> Solved problems -> Prove the following equality
Prove the following
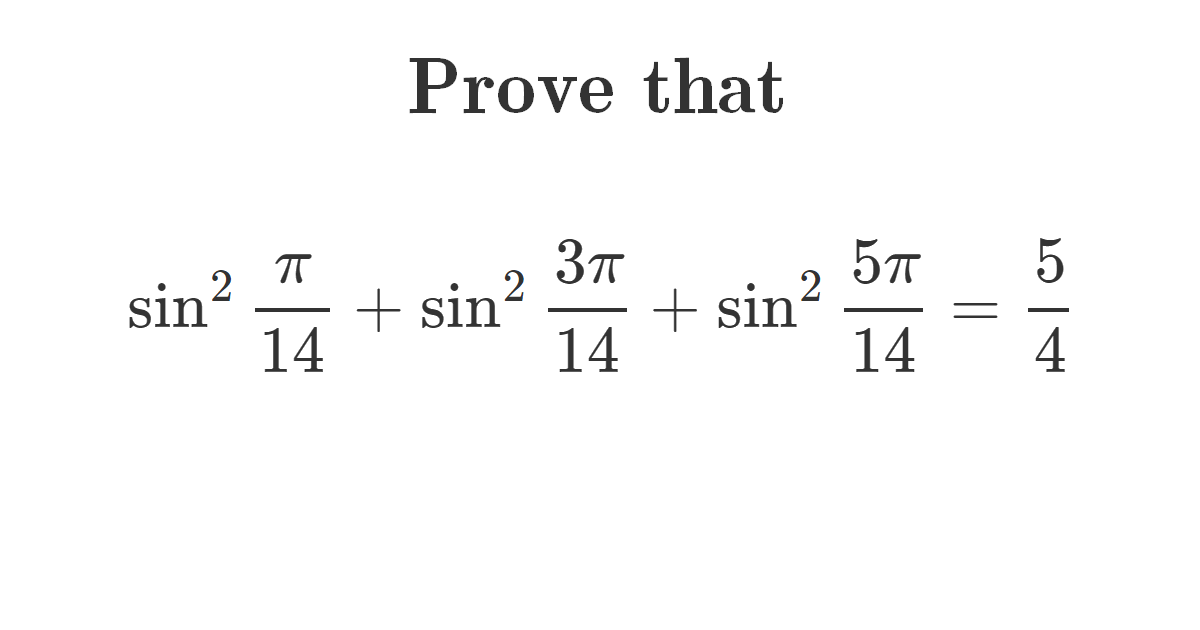
Solution
Let \(f\) be a function such that for \(x \in \mathbb{R}: f(x)=\cos 2 x+\cos 6 x+\cos 10 x\)
\[\begin{aligned}
&2 \sin 2 x f(x)=2 \sin 2 x \cdot \cos 2 x+2 \sin 2 x \cdot \cos 6 x+2 \sin 2 x \cos 10 x \\\\
&=\sin 4 x+\sin (2 x+6 x)+\sin (2 x-6 x)+\sin (2 x+10 x)+\sin (2 x-10 x) \\\\
&=\sin 4 x+\sin 8 x-\sin 4 x+\sin 12 x-\sin 8 x \\\\
&=\sin 12 x
\end{aligned}\]
\[\text { Let } x=\frac{\pi}{14}: 2 \sin \frac{2 \pi}{14} \cdot f\left(\frac{\pi}{14}\right)=\sin \frac{12 \pi}{14}\]
\[\begin{aligned}
&\Leftrightarrow 2 \sin \frac{\pi}{7} f\left(\frac{\pi}{14}\right)=\sin \frac{6 \pi}{7} \\\\
&\Leftrightarrow f\left(\frac{\pi}{14}\right)=\frac{\sin \frac{6 \pi}{7}}{2 \sin \frac{\pi}{7}}=\frac{\sin \left(\pi-\frac{\pi}{7}\right)}{2 \sin \frac{\pi}{7}}=\frac{\sin \frac{\pi}{7}}{2 \sin \frac{\pi}{7}}=\frac{1}{2}
\end{aligned}\]
\[\begin{aligned}
\sin ^{2} \frac{\pi}{14}+\sin ^{2} \frac{3 \pi}{14}+\sin ^{2} \frac{5 \pi}{14} &=\frac{1-\cos \frac{2 \pi}{14}}{2}+\frac{1-\cos \frac{6 \pi}{14}}{2}+\frac{1-\cos \frac{10 \pi}{14}}{2} \\\\
=& \frac{3-\left(\cos \frac{\pi}{7}+\cos \frac{3 \pi}{7}+\cos \frac{5 \pi}{7}\right)}{2}=\frac{3-f\left(\frac{\pi}{14}\right)}{2} \\\\
&=\frac{3-\frac{1}{2}}{2}=\frac{5}{4}
\end{aligned}\]
Home -> Solved problems -> Prove the following equality
Related Topics
Home -> Solved problems -> Prove the following equality
Share the solution: Prove the following equality